سوال 1.1.1 (-) حل کردم

در گراف زیر، درجه هر راس، تعداد راس ها، تعداد یال ها و $\delta , \Delta$ را مشخص کنید.

سوال 1.1.2 حل کردم

در یک مهمانی، ثابت کنید یا سه نفر وجود دارند که دو به دو با هم آشنا هستند و یا سه نفر وجود دارند که دو به دو با هم غریبه هستند.

سوال 1.1.3 (-) حل کردم

در یک مهمانی برخی با هم دست می دهند. از آن ها می خواهیم تا روی یک کاغذ بنویسند که با چند نفر دست داده اند و سپس اعداد نوشته شده را با هم جمع می زنیم. ثابت کنید حاصل به دست آمده یک عدد زوج است.

سوال 1.1.4 حل کردم

ابتدا یک گراف ۸ راسی بکشید که درجه تمام رئوس آن سه باشد، سپس ثابت کنید که نمی توان هیچ گراف ۹ راسی کشید که درجه تمام رئوس آن ۳ باشد.

سوال 1.1.5 (!) حل کردم

در یک گراف دلخواه، ثابت کنید $$ \delta \le \frac{2e}{n} \le \Delta $$

سوال 1.1.6 (+) حل کردم

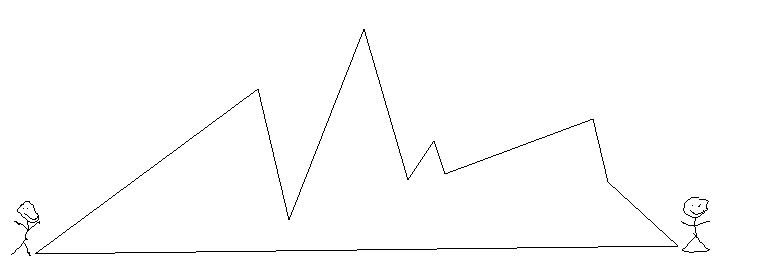
شیرین و فرهاد در دو سمت یک رشته کوه ایستاده اند. در این سوال ما رشته کوه را یک خط شکسته تعریف می کنیم که همواره بالای محور ایکس ها قرار دارد و دو سر آن (که شیرین و فرهاد در آن جا ایستاده اند) روی محور ایکس ها و در ارتفاع صفر قرار دارند. شیرین و فرهاد می خواهند همواره هم ارتفاع یک دیگر باشند و به هم برسند. آن ها می توانند روی رشته کوه عقب و جلو بروند. به کمک مدل سازی به گراف، ثابت کنید که آن ها همواره می توانند به هم برسند.

سوال 1.1.7 (!) حل کردم

اثبات یا رد کنید:

• حذف یک راس از درجه $\Delta$ نمی تواند میانگین درجات را زیاد کند
• حذف یک راس از درجه $\delta$ نمی تواند میانگین درجات را کم کند

سوال 1.1.8 (+) حل کردم

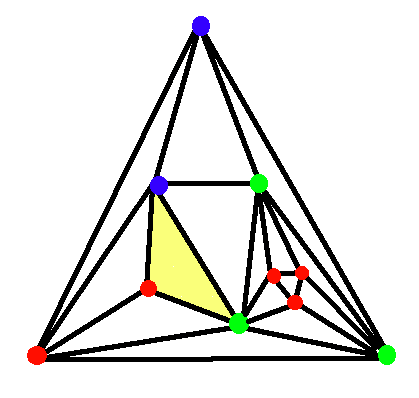
یک مثلث داریم که درون آن چند نقطه قرار داده شده است و سپس شکل مثلث بندی شده است، یعنی هیچ ناحیه ای درون مثلث وجود ندارد که مثلث نباشد. هر نقطه از این شکل با یکی از رنگ های آبی، قرمز و سبز رنگ شده است. می دانیم نقاط مثلث اصلی رنگ های متفاوتی دارند. ثابت کنید یکی از مثلث های کوچک وجود دارد که رئوس آن نیز رنگ های متفاوتی داشته باشند.

سوال 1.1.9 حل کردم

مثال نقضی برای گزاره زیر بیارید:

• در یک جمع با حداقل دو نفر آشنا که هر دو نفر با تعداد یکسانی آشنا در جمع هیچ آشنای مشترکی ندارند، یک نفر دقیقا با یک آشنا در جمع وجود دارد.

سوال 1.1.10 حل کردم

نشان دهید تعداد یال های یک گراف ساده حداکثر برابر جمع اعداد 1 تا n - 1 است.

سوال 1.1.11 حل کردم

رابطه بین دلتا کوچک و دلتا بزرگ گراف G و مکمل گراف G را مشخص کنید.

سوال 1.1.12 حل کردم

تعداد گراف های با رئوس ${1..n}$ که درجه تمام رئوس زوج هستند را بشمارید. دو گراف متفاوت در نظر گرفته می شوند اگر در یکی از آن ها دو راس به هم یال داشته باشند و در دیگری یال نداشته باشند.