Types of Graphs¶

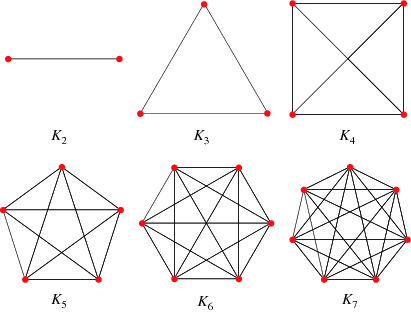
Complete Graph¶

A graph G is called a complete graph if for every two vertices u and v, there is an edge between them. It is denoted by \(K_n\).

Empty Graph¶

A graph G is called an empty graph if it contains no edges. In fact, an empty graph is the complement of a complete graph and is denoted by \(\overline{K_n}\).

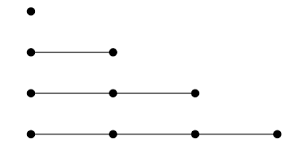
Path Graph¶

A graph G is called a path graph if it has n - 1 edges and the degree of its vertices is at most 2. A path graph is denoted by \(P_n\).

Cycle Graph¶

A graph G is called a cycle graph if the degree of all its vertices is 2, and it is possible to travel from any vertex to any other vertex by traversing a few edges. A cycle graph is denoted by \(C_n\).

Regular Graph¶

A graph in which the degree of all its vertices is equal is called a regular graph. If the degree of all vertices is equal to k, it is called a k-regular graph.

Petersen Graph¶

Unlike other sections which included many graphs, this section only includes one graph. How to construct the graph:

Consider a set of 5 elements. For every 3-element subset of this set, we place a vertex in the graph. We place an edge between two vertices if and only if their corresponding sets share exactly one common element.

The Petersen graph has 10 vertices and 15 edges, and the degree of each vertex is 3.

k-partite Graph¶

A graph is called a k-partite graph if its vertices can be partitioned into k sets such that for any two vertices u and v within the same set, there is no edge between them.

The smallest k for which a graph is k-partite is called its chromatic number and is denoted by the Greek letter chi as \(\chi\) or \(\chi (G)\).

Complete k-partite Graph¶

This is similar to the k-partite graph defined in the previous section, with the difference that there is an edge between any two vertices u and v that are not in the same partition. Complete k-partite graphs are denoted as \(K_{a_1,a_2,...,a_k}\). For example, the graph \(K_{a,b,c}\) is a complete tripartite graph whose partitions have a, b, and c vertices, and a total of \(a+b+c\) vertices.

Graph \(K_{3,5}\)

Graph \(K_{2,2,2}\)

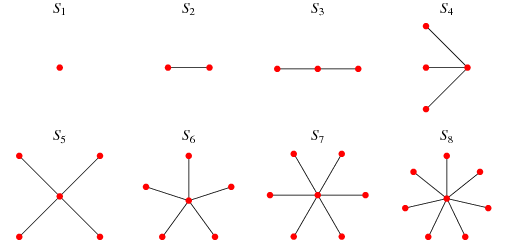
Star Graph¶

A graph G is called a star graph if there is one vertex u that is connected to all other vertices, and the other vertices are only connected to u. Since a star graph is a special case of a complete bipartite graph, it is represented as \(K_{1,n}\), which has \(n\) edges and \(n+1\) vertices.

k-dimensional Cube Graph¶

Consider all binary strings of length k. Each vertex of the graph is associated with one of these strings, such that each string is associated exactly once. Now, we place an edge between two vertices if and only if their corresponding strings differ in exactly one position. For example, if k = 3, the graph looks like this:

These graphs are denoted as \(Q_k\). \(Q_1\) resembles a line, \(Q_2\) resembles a square, and \(Q_3\) resembles a cube. The graph \(Q_k\) can be constructed by taking two copies of \(Q_{k-1}\) and placing an edge between their corresponding vertices. This property can help in proving the properties of these graphs. If you consider the binary code as k-dimensional coordinates, the graph \(Q_k\) forms a unit k-dimensional cube (in its generalized sense) whose corners align with the coordinate axes.