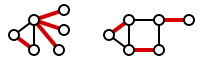
Introduction¶

Definition¶

A matching is a set of edges such that no two of them share a common vertex.

Mathematically, if we consider the graph as \(G\) and its set of edges as \(E\), a subset of \(E\) where no two members share a common vertex in \(G\) is called a matching or an independent set of edges, and it is denoted by \(M\).

A vertex that is an endpoint of an edge in a matching of graph \(G\) is called a saturated (matched) vertex, and otherwise, it is called an unsaturated (unmatched) vertex.

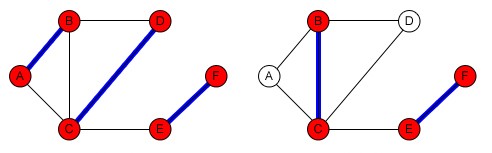
Maximal and Maximum Matching¶

A maximal matching is a matching in \(G\) such that if any other edge not in the matching is added to it, the resulting graph loses its matching property. In other words, a matching \(M\) is maximal if every edge in \(G\) intersects with at least one edge in \(M\).

A maximum matching is a matching that has the greatest number of edges in \(G\). Therefore, it can be concluded that every maximum matching is a maximal matching, but not every maximal matching is necessarily a maximum matching.

A perfect matching is also a matching in which all vertices are saturated (essentially, its number of edges is equal to \(|G| / 2\)). It can also be easily seen that a maximal matching is at least half the size of a maximum matching.

Alternating and Augmenting Paths¶

An alternating path is a path whose edges alternate between being in the matching and outside the matching.

An augmenting path is an alternating path whose first and last vertices are unsaturated and are not part of the matching.

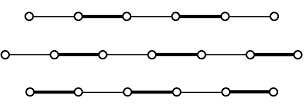
A matching is maximum if and only if it has no augmenting path, a conclusion also known as Berge's Theorem.

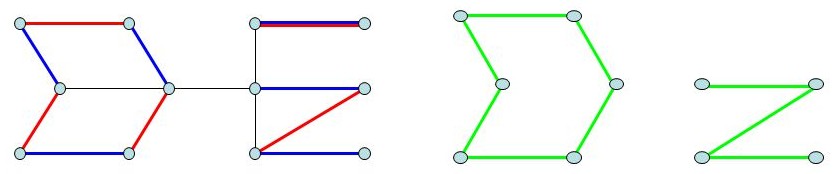
To prove that a maximum matching has no augmenting path, we can assume, for contradiction, that there is an augmenting path. Since an augmenting path is an alternating path and its first and last vertices are not in the matching, we can remove the matching edges within this path from the matching and add the other edges of this path to the matching instead. Because the first and last vertices are not in the matching, the number of non-matching edges in any augmenting path is one more than the number of matching edges. Thus, the matching size increases by one, creating a larger matching, which contradicts the assumption that the initial matching was maximum. Therefore, a maximum matching has no augmenting path.

The proof of the converse, i.e., if a matching has no augmenting path then it is maximum, can also be done by contradiction: Assume \(M'\) is a maximal matching with no augmenting path, and \(M\) is a maximum matching. Consider the graph \(M \Delta M'\). The degree of each vertex in it is at most two. Thus, this graph consists of a number of alternating cycles and paths. In cycles and even paths, the number of edges from both matchings is equal. In odd paths, the first and last edges must be from \(M\), because otherwise, we could use the edges from \(M'\) instead of \(M\) in the path and increase the size of the matching. So, if we have an odd path, it means we have at least one augmenting path, which is a contradiction. Therefore, we conclude that we have no odd paths, and \(|M| = |M'|\).

Vertex and Edge Cover¶

A set (cover) of vertices such that every edge has at least one of its endpoints in this set is called a vertex cover.

A set (cover) of edges such that every vertex has at least one of its incident edges in this set is called an edge cover.

A vertex cover with the minimum number of vertices is called a minimum vertex cover, and an edge cover with the minimum number of edges is called a minimum edge cover.