Strongly Connected Components¶

Definition 3.4.1 (Strongly Connected Pair of Vertices)¶

In a directed graph, a pair of vertices \((v, u)\) is said to be strongly connected if and only if there exists a path from \(v\) to \(u\) and a path from \(u\) to \(v\) .

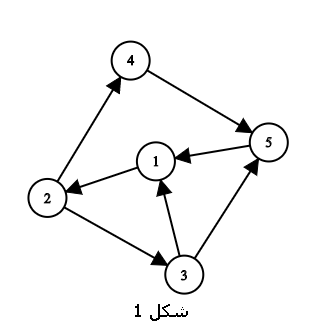
For example, in Figure 1, vertices 2 and 4 are a strongly connected pair.

Definition 3.4.2 (Strongly Connected Graph)¶

A strongly connected graph is a directed graph in which every pair of its vertices is strongly connected (Figure 1).

Definition 3.4.3 (Strongly Connected Component, or SCC)¶

A strongly connected component (SCC) in a directed graph \(G\) is a subset of vertices of \(G\) such that their induced subgraph forms a strongly connected graph, and it is also maximal, meaning no other vertex can be added to it.

Lemma 3.4.4¶

Statement: Every vertex \(v\) in a directed graph \(G\) belongs to exactly one unique strongly connected component.

Proof: We use proof by contradiction. Assume that \(v\) belongs to two strongly connected components \(H\) and \(L\) , and \(u\) is a vertex in \(L\) that is not in \(H\) . Since \(u\) and \(v\) are in a strongly connected component, it follows that from any vertex in \(H\) one can reach \(v\) via a path, and then reach \(u\) via another path. Similarly, one can come from \(u\) to \(v\) via a path, and then go to any desired vertex in \(H\) via another path. Therefore, vertex \(u\) could be added to component \(H\) , which contradicts the maximality of \(H\) . The contradiction proves the statement.

Corollary 3.4.5¶

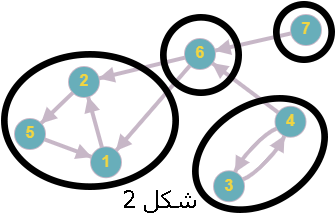
Any directed graph \(G\) can be partitioned into strongly connected components. Figure 2 shows a directed graph with its strongly connected components highlighted.

Definition 3.4.6 (Transpose Graph)¶

The transpose graph \(G^T\) is a graph obtained by reversing the direction of all edges in graph \(G\) . Note that a graph is strongly connected if and only if its transpose is also strongly connected.

Definition 3.4.7 (Condensed Graph of Strongly Connected Components)¶

Let \(G\) be an arbitrary directed graph, and let the directed graph \(H\) be a graph where each of its vertices corresponds to a strongly connected component in \(G\) , and each strongly connected component in \(G\) corresponds to exactly one vertex in \(H\) . If \(v\) is a vertex in \(H\) , we denote the strongly connected component corresponding to vertex \(v\) in \(G\) as \(F(v)\) . If \(v\) and \(u\) are two vertices of \(H\) , for every directed edge from a vertex in \(F(v)\) to a vertex in \(F(u)\) , there is a directed edge from \(v\) to \(u\) , and similarly, every edge from \(v\) to \(u\) corresponds to an edge from a vertex in \(F(v)\) to a vertex in \(F(u)\) . In this case, \(H\) is called the condensed graph of strongly connected components of \(G\) .

Theorem 3.4.8¶

Statement: Every condensed graph of strongly connected components is acyclic.

Proof: Let \(G\) be an arbitrary directed graph and \(H\) be the condensed graph of strongly connected components of \(G\) . We use proof by contradiction. Assume that \(H\) has a cycle, and two vertices, say \(v\) and \(u\) , from \(H\) are part of a cycle. Since there is a path from any vertex within a strongly connected component to any other vertex within that same component, it follows that one can go from any vertex in \(F(v)\) to any vertex in \(F(u)\) , and similarly, there exists a directed path from any vertex in \(F(u)\) to any vertex in \(F(v)\) (Why?). This implies that the vertices in \(F(v)\) and \(F(u)\) must belong to the same strongly connected component, which contradicts the assumption of maximality of the strongly connected components. Therefore, \(H\) has no cycles, and the statement is proven.

Corollary 3.4.9¶

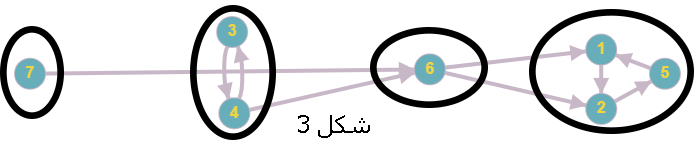
According to Theorem 3.3.2, the vertices of any condensed graph of strongly connected components can be topologically sorted. Consequently, the strongly connected components of any directed graph can be arranged in a topological sort order, meaning that all edges between two different components will point in a single direction (Figure 3).

Kosaraju's Algorithm¶

Description: First, we perform a \(DFS\) traversal on the entire graph, and each time we finish exploring a vertex, we push it onto a stack (note that the later a vertex is finished, the higher it is placed on the stack). Now, we consider the transpose graph. In each step, from all unvisited vertices, we pick the vertex that is highest in the stack (e.g., \(v\) ) and perform a \(DFS\) from it in the transpose graph. We then place \(v\) and all vertices visited (by performing \(DFS\) from vertex \(v\) ) into a new component. We continue this process until all strongly connected components are found. Note that when performing \(DFS\) on the transpose graph, once a vertex is visited, it is marked as visited, and we do not perform \(DFS\) from it or enter it in subsequent traversals.

Proof of Correctness: To prove this algorithm, first consider the following lemma, similar to one we had in the previous section.

Let's define \(f(v)\) as the finish time of the traversal for vertex \(v\) . In other words, we are determining a vertex's position in the stack (the greater \(f(v)\) is, the lower the vertex is placed in the stack).

Lemma 1: If \(f(u) > f(v)\) , meaning vertex \(u\) is higher in the stack than vertex \(v\) , and there is a path from \(v\) to \(u\) , then there is also a path from \(u\) to \(v\) .

Proof of Lemma 1: We use proof by contradiction. Assume there is a path from \(v\) to \(u\) , and no path from \(u\) to \(v\) .

Then, since we initially visited vertex \(u\) during the traversal (Why?), and there is no path from \(u\) to \(v\) , we will never traverse vertex \(v\) as part of \(u\) 's DFS path. On the other hand, if the traversal of vertex \(u\) finishes and we still haven't visited vertex \(v\) , it implies that \(u\) is added to the stack first, and then \(v\) , meaning \(f(u) < f(v)\) , which contradicts our assumption. Thus, the lemma is proven!

Now, note that when traversing the transpose graph, we move along the reversed edges. That is, we take the top element of the stack, which is vertex \(v\) , and traverse all vertices \(x\) such that there is a path from \(x\) to \(v\) (in the original graph). In this case, according to Lemma 1, vertex \(v\) also has a path to vertex \(x\) (in the original graph)!

Therefore, \(v\) and all vertices visited during the traversal of the transpose graph from \(v\) belong to a single component!

On the other hand, no other vertex is in this component. Otherwise, if another vertex were in this component, it would have to have at least one path to \(v\) (in G) and would have been counted among the vertices visited from \(v\) (in G^T).

Algorithm Complexity¶

In the above algorithm, we used \(DFS\) only twice. Consequently, the algorithm's complexity is \(O(n + m)\) , where \(n\) and \(m\) are the number of vertices and edges, respectively.

Lemma 3.4.10¶

Statement: Kosaraju's algorithm finds the strongly connected components in topological sort order.

Proof: We prove the statement by induction on the number of strongly connected components. For one component, the correctness of the statement is trivial. Now, assuming the statement holds for \(n-1\) components, we prove it for \(n\) components. If an edge enters the first component we find in the algorithm (say \(H\) ) from another component (say \(L\) ), then in the transpose graph, there is an edge from \(H\) to \(L\) . Since in the algorithm, \(L\) is found after \(H\) , it implies that during the traversal of \(H\) in the transpose graph, some vertices of \(L\) should be visited and placed within \(H\) , whereas components cannot overlap. Therefore, the first component we find has no incoming edges from other components and is the first component in the topological sort. Now, by the induction hypothesis, the remaining components are also found in topological sort order (Why?), and the statement is proven.

Algorithm Implementation¶

Note that at the end of the code, we output the components in their topological sort order.

const int MX = 5e5 + 5;

int n, m; /// number of vertices and edges
vector<int> gr[MX], back_gr[MX], comp[MX]; /// adjacency list, adjacency list (reversed edges), strongly connected components
stack<int> sk; /// sorting vertices based on DFS finish times
bool mark[MX]; /// mark array to check visited vertices

void dfs(int v){  /// normal DFS!
    mark[v] = 1;
    for(int u: gr[v])
                if(!mark[u])
                   dfs(u);
    sk.push(v);
}

void back_dfs(int v, int cnt){  /// DFS on reversed edges!
    mark[v] = 1;
    comp[cnt].push_back(v);
    for(int u: back_gr[v])
                if(!mark[u])
                    back_dfs(u, cnt);
}

int main(){
    cin >> n >> m;
    for(int i = 0; i < m; i++){
                int v, u;
                cin >> v >> u; /// vertex numbers are 0-based.
                gr[v].push_back(u); /// this vector stores edges
                back_gr[u].push_back(v); /// this vector stores reversed edges
    }
    for(int i = 0; i < n; i++)
                if(!mark[i])
                    dfs(i);
    fill(mark, mark + n, 0); /// since we want to start a new DFS, we reset mark to 0.
    int cnt = 0;
    while(sk.size() != 0){ /// stack is quite slow. Here, stack is used merely for better understanding. It's better to use a vector.
                if(!mark[sk.top()]){
                        back_dfs(sk.top(), cnt); /// we find one component
                        cnt++;
                }
                sk.pop();
    }
    /// we print the components in their topological sort order
    for(int i = 0; i < cnt; i++){
                cout << i << ": ";
                for(auto v: comp[i])
                        cout << v << ' ';
                cout << endl;
    }
    return 0;
}