Tournament¶
Definition 3.2.1 (Tournament)¶
A tournament is a simple, complete graph whose edges have been directed (Figure 1 shows a tournament with 5 vertices).
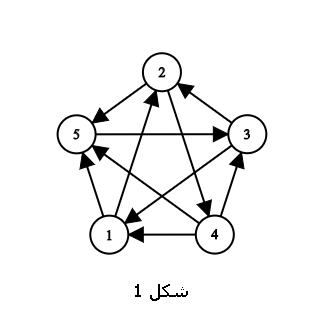
An \(n\)-vertex tournament can model competitions between \(n\) teams such that a directed edge from vertex 1 to vertex 2 exists if and only if team 1 has defeated team 2 (as in Figure 1).
Kings in Tournaments¶
Definition 3.2.2 (King)¶
A king is a vertex in a tournament that has a directed path of length at most 2 to all other vertices in the tournament. For example, vertex 3 is a king in Figure 1.
Theorem 3.2.3¶
Statement of the Theorem : Every tournament has at least one king.
Proof of the Theorem : Let \(v\) be a vertex with out-degree \(\Delta^{+}\) in the tournament, i.e., a vertex with the maximum out-degree. If there exists a vertex \(u\) such that there is no path of length at most 2 from \(v\) to \(u\), then \(u\) must have a directed edge to \(v\) and to all vertices \(w\) such that \((v,w) \in E\) (Figure 2). In this case, \(d^{+}(u) \geq \Delta^{+}+1\), which contradicts the maximality of the out-degree of \(v\). Therefore, no such vertex \(u\) exists that cannot be reached from \(v\) by at most two edges, and thus \(v\) is a king.
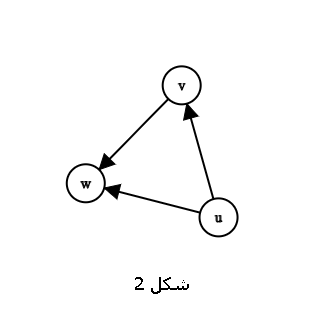
Theorem 3.2.3 implies that, for example, in a tournament of competitions, there exists an individual \(v\) such that for every other individual \(u\), either \(v\) has defeated \(u\), or \(v\) has defeated someone who has defeated \(u\).
Hamiltonian Paths in Tournaments¶
Definition 3.2.4 (Hamiltonian Path in a Directed Graph)¶
A Hamiltonian path in a directed graph is a directed path that passes through all vertices.
Theorem 3.2.5¶
Statement of the Theorem : Every tournament has at least one Hamiltonian path.
Proof of the Theorem : Let vertices \(a_1\) to \(a_k\) form the longest directed path in the tournament (Figure 3).
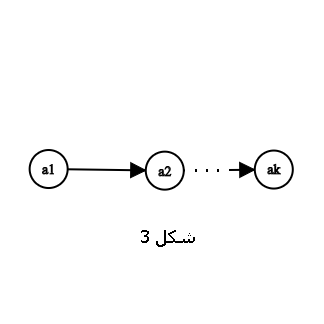
If \(k = n\), the theorem is proven. Otherwise, there exists a vertex \(v\) that is not on this path. There cannot be a directed edge from \(v\) to \(a_1\) and from \(a_k\) to \(v\) (why?). So, assume \(a_i\) is the vertex with the smallest \(i\) among all vertices from \(a_1\) to \(a_k\) such that \(v\) has an edge to \(a_i\). In this case, the vertices \(a_1,...,a_{i-1},v,a_i,...,a_k\) form a path of length \(k+1\), which contradicts the assumption that the longest path has length \(k\). Therefore, \(k = n\), and \(a_1\) to \(a_k\) form a Hamiltonian path.
