Segment Tree¶

Structure¶

Each node in this tree represents a range of the queried array. The children of each node (if they exist, naturally there are two) divide their parent's range in half, or in other words, if a node's range is \([Begin, End)\), the ranges of its two left and right children are \([Begin, Middle)\) and \([Middle, End)\) respectively. Leaf nodes (nodes without children) contain a single element from the array.

To better understand the relationship between nodes and ranges, refer to the figure below.

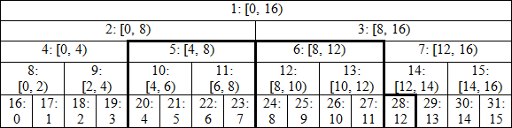
In each of these nodes, specific information about the corresponding range in the array is available, which can vary depending on our use of this data structure. For example, if we are looking for the sum of a range in an array, each node stores the sum of its corresponding range.

For a better understanding of this part, observe how each node stores a value in the figure below.

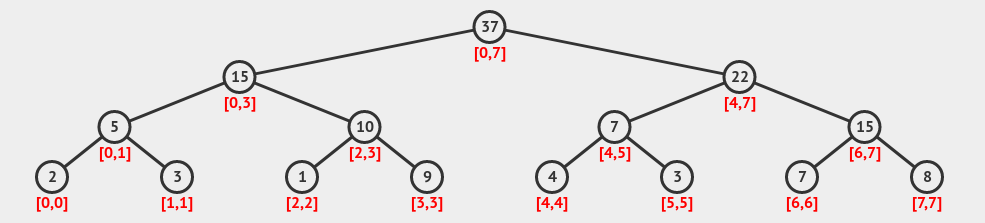
The height of this tree is \(lg n\) and the maximum number of nodes it uses is \(2n\), so you can store this data structure with \(2n\) memory. It's worth noting that some people consider \(4n\) memory, which is due to an implementation style where two children without any specific attributes are placed for each leaf node (single-element nodes), causing the memory usage to double.

For numbering the nodes, the root can be assigned the number one, and the left and right children of each node can be assigned \(2k\) and \(2k + 1\) respectively.

Algorithm¶

The execution method of this algorithm is almost identical for all types of problems solvable with this data structure, and we will explain it using one of the well-known queries for this data structure.

Initially, an array is given to us, and at each step, we are asked either to change the value of an array element or to report the sum of a range.

void build(int u = 1, int ul = 0, int ur = n){
    if(ur - ul < 2){
        seg[u] = a[ul];
        return;
    }
    int mid = (ul + ur) / 2;
    build(u * 2, ul, mid);
    build(u * 2 + 1, mid, ur);
    seg[u] = seg[u * 2] + seg[u * 2 + 1];
}

void update(int i, int x, int u = 1, int ul = 0, int ur = n){
    seg[u] += x - a[i];
    if(ur - ul < 2){
        a[i] = x;
        return;
    }
    int mid = (ul + ur)/2;
    if(i < mid)
        update(i, x, u * 2, ul, mid);
    else
        update(i, x, u * 2 + 1, mid, ur);
}

int sum(int l, int r, int u = 1, int ul = 0, int ur = n){
    if(x >= ur || ul >= y)return 0;
    if(x <= ul && ur <= y)return seg[u];
    int mid = (ul + ur) / 2;
    return sum(l, r, u * 2, ul, mid) + sum(l, r, u * 2 + 1, mid, ur);
}

Lazy propagation¶

Suppose that in the first operation, instead of changing a single value, changing a range is concerned. For example, we are asked to add two units to the range \(L\) to \(R\). If we want to change all elements in this range, it's difficult and the number of operations increases. Now, using the lazy propagation technique, we can reduce the number of operations. This is done by considering an additional value for each node, which is stored in a lazy array, for example. We partition the given range for modification into smaller ranges (on the tree), similar to how we handled the queried range in the second operation, and change the lazy array value for all these nodes (nodes on which the range has been partitioned). And whenever we are at a node in the tree during this algorithm, we add its lazy value to the node's own value, add its lazy value to its children's lazy values, and then zero it out.

void upd(int u, int ul, int ur, int x){
    lazy[u] += x;
    seg[u] += (ur - ul) * x;
}
void shift(int u, int ul, int ur){
    int mid = (ul + ur) / 2;
    upd(u * 2, ul, mid, lazy[u]);
    upd(u * 2 + 1, mid, ur, lazy[u]);
    lazy[u] = 0;
}
void increase(int l, int r, int x, int u = 1, int ul = 0, int ur = n){
    if(l >= ur || ul >= r)return;
    if(l <= ul && ur <= r){
        upd(u, ul, ur, x);
        return;
    }
    shift(u, ul, ur);
    int mid = (ul + ur) / 2;
    increase(l, r, x, u * 2, ul, mid);
    increase(l, r, x, u * 2 + 1, mid, ur);
    seg[u] = seg[u * 2] + seg[u * 2 + 1];
}
int sum(int l, int r, int u = 1, int ul = 0, int ur = n){
    if(l >= ur || ul >= r)return 0;
    if(l <= ul && ur <= r)return seg[u];
    shift(u, ul, ur);
    int mid = (ul + ur) / 2;
    return sum(l, r, u * 2, ul, mid) + sum(l, r, u * 2 + 1, mid, ur);
}