Degree Sequence¶
Consider an \(n\)-vertex graph \(G\).
Let the degree of vertex \(i\) be denoted by \(d_{i}\). Then the sequence \(d_{1}, d_{2}, ..., d_{n}\) is called the degree sequence of graph \(G\).
Graphic Sequence¶
A sequence \(d_{1}, d_{2}, ..., d_{n}\) is called a graphic sequence if there exists a simple \(n\)-vertex graph \(G\) such that its vertex degree sequence is equal to the given sequence.
Havel-Hakimi Algorithm¶
This algorithm is used to determine if a sequence is graphic. It is a greedy algorithm that, at each step, connects the vertex with the largest degree to the next largest degree vertices. If, at any step, we are forced to connect an edge to a vertex with degree zero, it means our sequence is not graphic. The correctness of this greedy algorithm is equivalent to the theorem stating that a sorted sequence \(d_{1}, d_{2}, ..., d_{n}\), where \(d_{1} \ge d_{2} \ge ... \ge d_{n}\), is graphic if and only if \(d_{2} - 1 , d_{3} -1 , ... d_{d_1+1} -1, d_{d_1+2}, ... , d_{n}\) is graphic.
2-Switch Operation¶
In the context of proving the Havel-Hakimi theorem, we define the 2-switch operation between 4 vertices \(a, b, c, d\) as follows: assume there are edges between \(a, b\) and \(c, d\), and there are no edges between \(a, c\) and \(b, d\).
In this case, we remove edges \(a, b\) and \(c, d\) from the graph and add edges \(a, c\) and \(b, d\). For a better understanding, refer to the figure below.
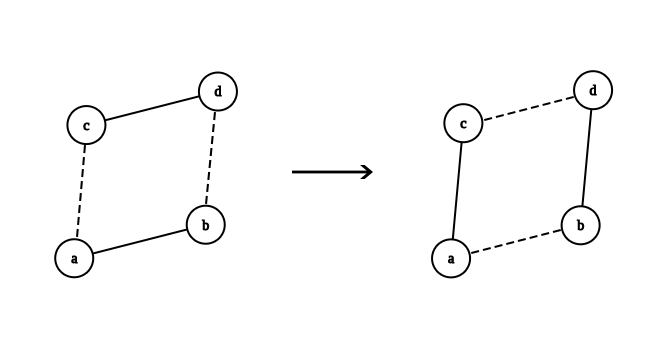
The important point about this transformation is that, by applying it, the degree sequence of the graph remains unchanged.
Proof of the Theorem¶
One direction of this theorem is trivial, because if the sequence \(d_{2} - 1 , d_{3} -1 , ... d_{d_1+1} -1, d_{d_1+2}, ... , d_{n}\) is graphic, by considering its corresponding graph and adding a vertex, it can be shown that the original sequence was also graphic.
Now we prove the other direction. By assumption, the original sequence is graphic, and we must prove that the sequence \(d_{2} - 1 , d_{3} -1 , ... d_{d_1+1} -1, d_{d_1+2}, ... , d_{n}\) is also graphic. Among all graphs that have a degree sequence equal to our sequence, consider one where vertex number one is connected to the maximum number of vertices from \(v_{2} , v_{3} , ... v_{d_1+1}\), which we will henceforth call "good vertices", and the rest "bad vertices". If vertex number one is connected to all good vertices, by removing it, the desired graph is constructed, and the statement holds. Otherwise, consider a good vertex that is not connected to vertex one, and a bad vertex that is connected to vertex one. If the good vertex has a neighbor that is not adjacent to the bad vertex, a 2-switch operation can be performed on these four vertices, thereby increasing the number of good vertices adjacent to vertex one by one, which contradicts the extremal assumption. Otherwise, all neighbors of the good vertex are also neighbors of the bad vertex, and furthermore, the bad vertex is also adjacent to vertex one. Therefore, the degree of the bad vertex is strictly greater than that of the good vertex, which contradicts the assumption that the degrees are sorted. Thus, the statement is proven, meaning the desired sequence is graphic.
This book is made by The Shaazzz contributors.
It is publicly available with cc-by-sa license.
Last updated at اکتبر 13, 2025.
Rendered by Sphinx (4.3.2) and Minoo theme (Beta 0.9.7).
