Huffman Coding¶

Character to 0,1 Correspondence¶

The process of converting a sequence of characters into a sequence of 0s and 1s is called encoding, and the reverse process (converting a sequence of 0s and 1s back into characters) is called decoding.

The first question that comes to mind is how to map each character to a binary sequence so that the decoding operation is unique and correct. A clever idea here is to use trees. We define a binary rooted tree and call it an encoding tree, which has the following properties:

• Each node in this tree has at most two children. For each node, we have written the numbers 0,1 on the edges leading to its children (0 for the left child and 1 for the right child).

• Each leaf of this tree (the root is never considered a leaf) will correspond to one of our alphabet characters.

In this case, for each alphabet character \(x\), assume \(u\) is the leaf corresponding to \(x\). Then, assign the sequence of 0,1s seen from the root to node \(u\) as the code for character \(x\).

Now, how can a binary text be decoded? Simply place a token on the root node and start reading the binary text. If you see a 0, move to the left edge; if you see a 1, move to the right edge until you reach a leaf that corresponds to a character. This means that the first character of our text is the character we reached. (Note that no non-leaf node corresponds to a character, so the first character of the text could not have been any other character). Then, return the token to the root and start reading the binary string again to determine the second character of the original string. By continuing this process, the string can be decoded. If, during this process, the token was supposed to move to an edge that does not exist (e.g., if a 0 was read but there was no left edge) or if, at the end, the token is not at the root, it means our binary text is incorrect, and no original text exists that would be encoded into this string.

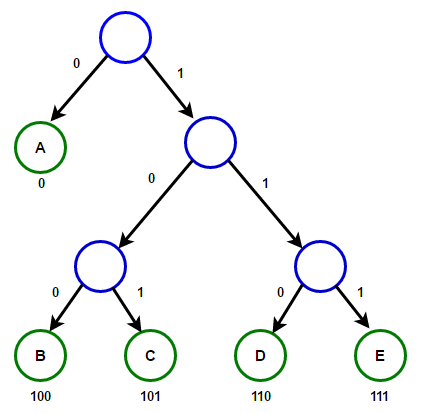
An Optimal Tree¶

Now that we know that character-to-binary string mapping can be done by constructing an encoding tree, we return to the main problem. Our goal now is to provide an encoding tree that minimizes the length of our encoded binary string.

More precisely, suppose we want to provide an encoding tree that converts text \(s\) into binary sequence \(p\) such that the length of \(p\) is minimized. Assume that for the \(i\)-th character, we have \(c_i\) occurrences in string \(s\). Now, the length of \(p\) will be \(\sum h_i \times c_i\), so we want to minimize this value.

Let \(T\) be the desired encoding tree. Pay attention to the following points:

• If we sort characters based on their frequencies (\(c_i\)) from low to high, then their code lengths (\(h_i\)) will be sorted from high to low. (Otherwise, we could swap the nodes corresponding to two characters to reduce the length of \(p\)).

• All leaves have siblings (unless there is only one leaf). Otherwise, that leaf could be removed, and the character assigned to it could be assigned to its parent. In this case, the length of \(p\) would decrease.

• If two leaves \(a\) and \(b\) are at the same depth, the characters assigned to \(a\) and \(b\) can be swapped without changing the length of \(p\).

Thus, it can be concluded that if we consider the two characters with the minimum frequencies, \(x\) and \(y\), they will be at the lowest depth of the tree. Furthermore, their corresponding nodes can be arranged such that they are siblings!

So, an optimal state exists where the leaves corresponding to \(x,y\) are two siblings at the lowest depth of the tree. Assume the depth of the nodes corresponding to \(x,y\) is \(h\). Since the binary strings corresponding to \(x,y\) differ only in the last digit (i.e., the \(h\)-th digit), it can be understood that the \(h\)-th digit appears a total of \(c_x + c_y\) times for both.

Next, we can remove the two characters \(x\) and \(y\) and define a new character, say \(z\), which replaces \(x,y\). The node corresponding to \(z\) will be the common parent of \(x,y\). Thus, we have reduced the number of alphabet characters by one, and the problem can be solved recursively for them. If we assume the answer to the new problem (minimum length of \(p\)) is \(ans ^ {\prime}\), then our current problem's answer will be \(ans = ans ^ {\prime} + c_x + c_y\).

You can also see that the optimal tree \(T\), which we had assumed to exist, will be built automatically during the algorithm's steps!

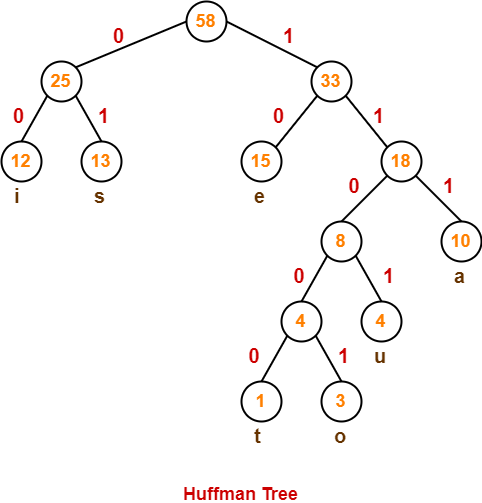
So, the algorithm is as follows: at each step, combine the two characters with the lowest frequencies (e.g., \(x,y\)) and replace them with a new character whose frequency is \(c_x + c_y\), then add \(c_x + c_y\) to the total answer.

You can see the implementation of this algorithm below.

typedef pair<int, int> pii;

const int maxn = 1e5 + 10;

vector<int> Tree[maxn]; // children of each node in the encoding tree

int c[maxn]; // frequency of each character
int Counter; // keeps track of the lowest unused node ID
priority_queue<pii, vector<pii>, greater<pii> > pq; // a min-heap

int main(){
    int n; // number of alphabet characters
    cin >> n;
    for(int i = 0; i < n; i++){
          cin >> c[i];
           pq.push({c[i], i});
    }
    Counter = n;
    int ans = 0;
    while(pq.size() > 1){
       int x = pq.top().second, y = pq.top().second; // This line might have a bug. It should pop twice.
       pq.pop(), y = pq.top().second; // Corrected: pop x, then get y and pop it.
       pq.pop(); // Pop y after getting its value.
       int z = Counter;
       Counter++;
       Tree[z].push_back(x);
       Tree[z].push_back(y);
       c[z] = c[x] + c[y];
       ans+= c[x] + c[y];
       pq.push({c[z], z});
    }
    // Here, ans is the minimum length of p, and we have built an optimal encoding tree in Tree.
}