Planar Graph¶
A planar graph is a graph that can be drawn on a plane without its edges crossing each other. The following graphs are planar:
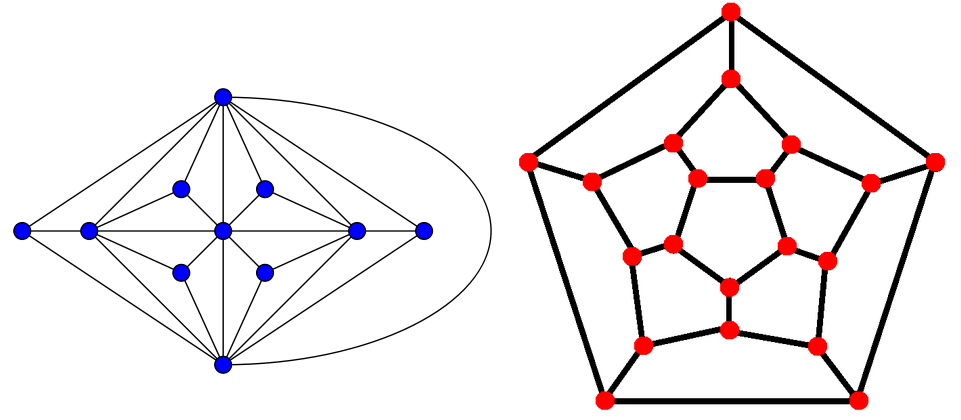
A graph that cannot be drawn on a plane in this way is a non-planar graph. For example, the complete graph with five vertices is non-planar. (Try it yourself :) )
Drawing a Planar Graph on a Sphere¶
A graph can be drawn on a sphere such that its edges do not intersect if and only if it is planar. For the proof, we use the following transformation.
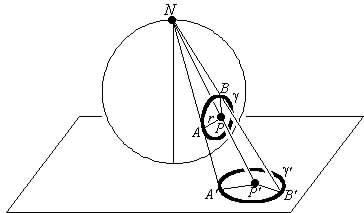
Place a sphere on a plane and consider the pole opposite to the point of tangency with the plane. (Point N) Any line containing this point covers exactly one point from the plane and one point from the sphere. Now, to prove the theorem, consider a planar graph on the plane and draw it on the sphere. This is done by drawing a line from N to each point on the plane and finding its equivalent point on the sphere. If that point on the plane was a vertex, place a vertex on the sphere; if it was an edge, a point on the edge; and if it was a face, a point on the face. In this way, a drawing of the graph on the sphere is obtained. It can be seen that the edges do not lose their continuity and it is obvious that they do not intersect each other.
For the other direction of the theorem, we proceed similarly. However, we make sure that point N is not on a vertex or an edge. The region containing that point becomes the infinite region surrounding the graph.
Euler's Theorem¶
Euler's Theorem is a relation for determining the number of faces formed in a planar graph. This theorem states that:
where f is the number of faces, e is the number of edges, t is the number of components, and n is the number of vertices. Specifically, in a connected graph, we have:
Proof¶
The proof of this theorem is not complicated at all, so it's good to think about it yourself first. If the graph is a forest, the statement holds because there is one face, and we have \(e = n - t\). But if it is not a forest, we remove one of the edges that is part of a cycle and is not a cut edge. The number of vertices and components remains constant, but the number of faces and the number of edges decrease by exactly one. So, if the statement is true for the new graph, it was also true for the previous graph. We continue this process until we reach a forest. Since the statement holds for a forest, it has also held for all graphs in between, including the initial graph.
Dual Graph¶
The dual graph of a planar graph is obtained as follows: place a vertex in each face, then draw an edge between vertices corresponding to adjacent faces. Like the figure below:
Note that the dual graph is also planar. Dual graphs can be useful in solving problems related to planar graphs.
Maximal Planar Graph¶
A maximal planar graph is a simple planar graph to which no more edges can be added while keeping it simple and planar. A graph with more than two vertices is maximal if and only if every face has three edges, or in other words, its dual graph is 3-regular. In a maximal planar graph, we have:
which, if we substitute it into Euler's relation (a maximal planar graph is clearly connected), yields:
which proves that in any simple planar graph
This book is made by The Shaazzz contributors.
It is publicly available with cc-by-sa license.
Last updated at اکتبر 13, 2025.
Rendered by Sphinx (4.3.2) and Minoo theme (Beta 0.9.7).
