Incidence Matrix¶

Incidence Matrix¶

In simple graphs, it's an n × m matrix where \(a_{ij}\) is one if vertex i is an endpoint of edge j, and zero otherwise. All entries of this matrix are zero or one.

If multiple edges also exist, the incidence matrix will not encounter a problem, as only the number of columns increases, and it does not change the structure or overall nature of the incidence matrix. However, if we have loops, the situation is slightly different because a vertex with a loop takes the value two instead of one; that is, \(a_{ij}\) takes the value two if vertex i has loop j.

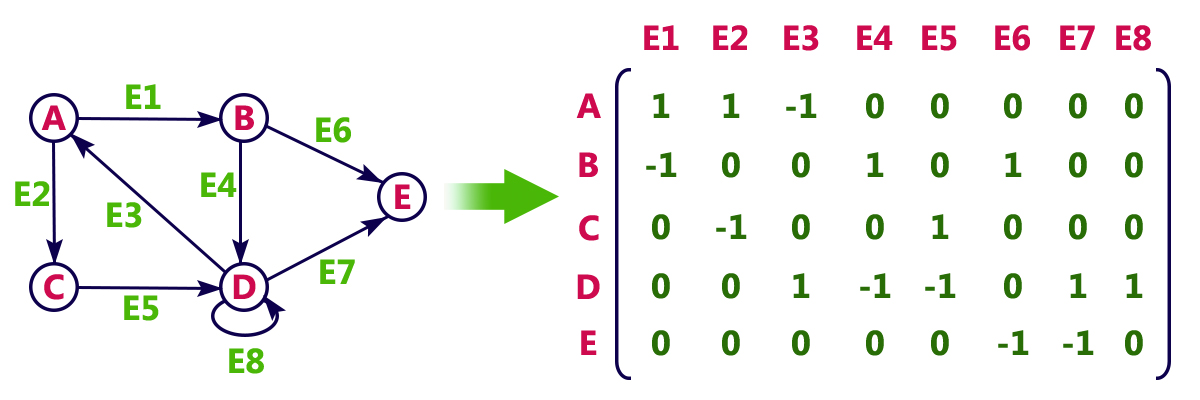
In directed graphs, a different structure appears in the incidence matrix. In this way, \(a_{ij}\) takes the value one if edge j exits vertex i or if edge j is a loop, takes the value negative one if edge j enters vertex i, and takes the value zero if none of the above conditions are met. The sum of the values in the incidence matrix of a directed graph gives us the number of loops.