Matching in Bipartite Graphs¶

Algorithm¶

In this algorithm, we start with an empty matching and enlarge it as long as an augmenting path exists in the graph. It is easily observable that the maximality of our final matching is then trivial. To find an augmenting path, we proceed as follows:

Suppose our graph consists of two partitions with \(n_1\) vertices and \(n_2\) vertices. For each vertex \(v = 1 ... n_1\) in our current graph, we search for an augmenting path. In the \(i\)-th step, we can claim that the matching between the \(i\) vertices of the first partition and the rest of the vertices in the second partition is maximum; consequently, our final matching will also be maximum. Its implementation is as follows:

const int N = 2e3 + 5;
int n1, n2, m, k, match[N];
vector <int> adj[N];
bool mark[N];

bool try_kuhn(int u){
    mark[u] = true;
    for(auto v: adj[u])
        if(match[v] == -1 || (!mark[match[v]] && try_kuhn(match[v]))){
            match[v] = u;
            return true;
        }
    return false;
}

void read_input(){
    cin >> n1 >> n2 >> m;
    for(int i = 0; i < m; i++){
        int u, v;
        cin >> u >> v;
        adj[--u].push_back(--v);
    }
}

void calc(){
    memset(match, -1, sizeof match);
    for(int u = 0; u < n1; u++){
        memset(mark, false, sizeof mark);
        k += try_kuhn(u);
    }
}

void write_output(){
    cout << k << endl;
    for(int u = 0; u < n2; u++)
        if (match[u] != -1)
            cout << match[u] + 1 << ' ' << u + 1 << endl;
}

int main() {
    read_input();
    calc();
    write_output();
    return 0;
}

In the algorithm mentioned, for each vertex in the first partition, \(O(m)\) steps are performed, so its time complexity is \(O(nm)\). However, there is another implementation of this same algorithm that is at least twice as fast as the one above (why?):

const int N = 2e3 + 5;
int n1, n2, m, k, match[N];
vector <int> adj[N];
bool mark[N];

bool try_kuhn(int u){
    mark[u] = true;
    for(auto v: adj[u])
        if (match[v] == -1 || (!mark[match[v]] && try_kuhn(match[v]))) {
            match[v] = u;
            return true;
        }
    return false;
}

void read_input(){
    cin >> n1 >> n2 >> m;
    for(int i = 0; i < m; i++){
        int u, v;
        cin >> u >> v;
        adj[--u].push_back(--v);
    }
}

void calc(){
    memset(match, -1, sizeof match);
    while(true){
        bool flag = false;
        memset(mark, false, sizeof mark);
        for(int u = 0; u < n1; u++)
            if (!mark[u])
                k += try_kuhn(u);
        if (!flag)
            break;
    }
}

void write_output(){
    cout << k << endl;
    for (int u = 0; u < n2; u++)
        if (match[u] != -1)
            cout << match[u] + 1 << ' ' << u + 1 << endl;
}

int main(){
    read_input();
    calc();
    write_output();
    return 0;
}

Hall's Theorem¶

This theorem states another necessary and sufficient condition for a maximum matching in a bipartite graph, which was first introduced by Philip Hall and is known as the Marriage Theorem. This theorem is as follows:

Let \(X\) be a set of vertices in the first partition of a bipartite graph. The set \(X\) has a perfect matching in the graph if and only if for every subset \(S\) of \(X\) and their neighbors outside \(X\) in the graph, named \(T\), we have \(|S| \leq |T|\).

The necessity of the above condition is trivial (otherwise, the number of neighbors of a set would not be sufficient to match them). To prove sufficiency, we use proof by contradiction and assume there exists a graph with such a property that does not have a perfect matching;

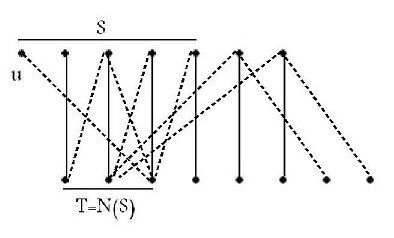
We consider a maximum matching and an arbitrary unsaturated vertex, say \(u\) (which must exist!). Since this vertex is not matched with anyone, we consider the matched vertex of an arbitrary neighbor of \(u\). These two vertices, according to the problem assumption, have another neighbor which is either unmatched (in which case we have an augmenting path) or matched, in which case we add its matched vertex to these two vertices. We continue this process as far as possible, and since the number of neighbors of \(X\) is at least their own size, we eventually reach a stage where our current set has an unmatched neighbor, which means we have an augmenting path. This contradicts the maximality of our matching.

Matching in k-Regular Bipartite Graphs¶

According to Hall's theorem, it can be proven that a k-regular bipartite graph has a perfect matching. To prove this, it suffices to show that Hall's condition holds for it;

Consider a set of vertices from the first partition of the graph, say \(S\), and call their neighbors in the second partition \(T\). We prove that \(|S| \leq |T|\). We know that the sum of edges between the two partitions is \(x = |S| \times k\). From this relationship, we can deduce that \(|T| \geq (x \div k) = |S|\).

Thus, Hall's condition holds in our graph, and a perfect matching is definitely found in our graph.

Generalization of Hall's Theorem¶

We have a bipartite graph named \(G\) and want to remove some of its edges such that the degree of each vertex in the first partition, say \(u\), becomes \(a_u\), and the degree of each vertex in the second partition becomes at most one. To solve this problem, we construct a graph \(G'\) such that a perfect matching from the first partition to the second exists in it if and only if such a set of edges exists in graph \(G\);

We construct graph \(G'\) such that for each vertex \(u\) in the first partition of graph \(G\), we create a set of \(a_u\) vertices (which are copies of vertex \(u\)), and for each edge \((u, v)\) in graph \(G\), we connect all vertices in the set corresponding to \(u\) to vertex \(v\). The resulting graph is bipartite (why?). If Hall's condition holds in it, meaning it has a perfect matching, then for each edge between the set of vertices corresponding to \(u\) and vertex \(v\) in \(G'\), we remove the edge \((u, v)\) in graph \(G\). It is clear that in this case, we obtain our desired set of edges. Similarly, if graph \(G'\) does not have a perfect matching, it can be concluded that no such set exists in graph \(G\) either (we proceed in reverse).

Consider the process of checking Hall's condition in graph \(G^{\prime}\). For every subset \(S\) from the first partition of graph \(G ^ {\prime}\) and its set of neighbors \(T\), we check if \(|S| \leq |T|\) holds. Now, it can be noted that for any vertex \(u\), if some copies of \(u\) are included in \(S\) but not all of them, we can add all copies to set \(S\). In this case, \(T\) will not change, and only \(S\) will increase. Therefore, we only need to check subsets \(S\) where for each \(u\), either all copies of \(u\) are included, or none are.

With a bit of thought, we conclude that according to the above statements, this necessary and sufficient condition can be found for graph \(G\): \(\forall_{S} \sum\limits_{i \in S} a_i \leq |T|\)

where \(S\) is any subset of vertices from the first partition of the graph, and \(T\) is the union of neighbors of \(S\).