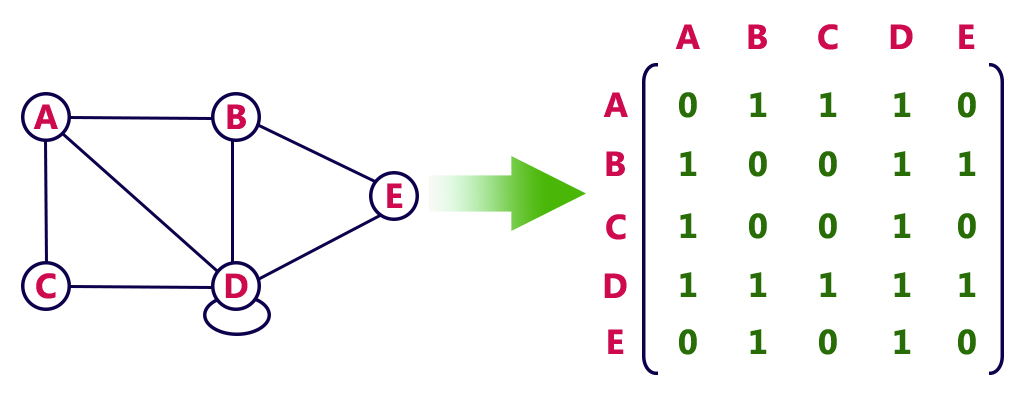
Adjacency Matrix¶
Adjacency Matrix¶
The adjacency matrix is an n × n matrix used to represent simple graphs. In this matrix, \(a_{ij}\) represents the number of edges between vertex i and vertex j in the graph. If you observe, you'll notice that this matrix is symmetric. The entries of this matrix are either zero or one.
In Graphs with Multiple Edges and Loops¶
In these graphs, the adjacency matrix is used with its original definition, the difference being that the entries are no longer necessarily zero or one and can take any non-negative integer value.
In Directed Graphs¶
In directed graphs, the adjacency matrix is defined such that \(a_{ij}\) represents the number of edges going from vertex i to j.
A final point regarding the adjacency matrix is that it is not used when the graph has weights, although a matrix similar to it is used in finding shortest paths, and in all the definitions above, the edges are unweighted.
This book is made by The Shaazzz contributors.
It is publicly available with cc-by-sa license.
Last updated at اکتبر 13, 2025.
Rendered by Sphinx (4.3.2) and Minoo theme (Beta 0.9.7).
