هافمن کدینگ¶

تناظر حروف به 0,1¶

به فرایند تبدیل دنباله ای از حروف به دنباله ای از 0,1 ها رمزگذاری می گوییم و به برعکس این فرایند (یعنی تبدیل دنباله 0,1 ها به دنباله حروف) رمزگشایی می گوییم.

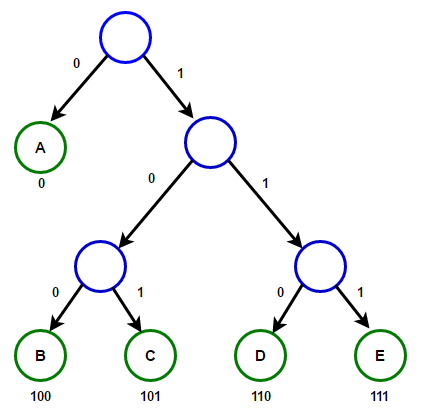
اولین سوالی که در ذهنمان پیش می آید این است که چگونه هر حرف را به یک دنباله دودویی تناظر دهیم تا عملیات رمزگشایی به صورت یکتا و درست انجام شود؟ یک ایده هوشمندانه در اینجا استفاده از درخت ها است. یک درخت ریشه دودویی تعریف می کنیم و به آن درخت رمزگذاری می گوییم که خاصیت های زیر را دارد.

• هر راس این درخت حداکثر دو بچه دارد. به ازای هر راس روی یال های این راس که به بچه هایش می رود عدد 0,1 نوشته ایم (0 برای بچه چپ و 1 برای بچه راست).
• هر برگ این درخت (ریشه هیچگاه برگ محسوب نمی شود) متناظر با یکی از حروف الفبای ما خواهد بود.

در اینصورت به ازای هر حرف \(x\) الفبا فرض کنید \(u\) برگ متناظر با \(x\) باشد. در اینصورت دنباله 0,1 هایی که از ریشه تا راس \(u\) می بینیم را متناظر با حرف \(x\) قرار دهید.

حالا چگونه می توان یک متن دودویی را رمزگشایی کرد؟ کافی است ابتدا یک مهره را روی راس ریشه قرار دهید و شروع به خواندن متن دودویی کنید. سپس اگر 0 دیدید به یال سمت چپ بروید و اگر 1 دیدید به یال سمت راست بروید تا زمانی که به یک برگ برسید که به یک حرف متناظر شده است. و به این معنی است که حرف اول متنمان همان حرفی است که به آن رسیدیم. (دقت کنید که هیچ راس غیربرگی به حروف متناظر نشده پس اولین حرف متن نمی توانسته هیچ حرف دیگری باشد). سپس دوباره مهره را به ریشه برگردانید و دوباره شروع به خواندن رشته دودویی کنید تا حرف دوم رشته اصلی را متوجه شوید. با ادامه این فرایند می توان رشته را رمزگشایی کرد. اگر در این فرایند ها مهره می خواست به یالی برود که وجود ندارد‌ (مثلا اگر 0 نوشته شده بود ولی یال سمت چپ نداشتیم) یا اگر در آخر کار مهره روی ریشه نباشد به این معنی است که متن دودویی ما اشتباه است و هیچ متنی وجود ندارد که بعد از رمزگذاری به این رشته تبدیل شود.

یک درخت کمینه¶

حال با دانستن اینکه می توان تناظر حروف به رشته های دودویی را با ساختن یک درخت رمزگذاری انجام داد، به مسئله اصلی بر می گردیم. حالا هدف ما این است که یک درخت رمزگذاری ارائه دهیم که طول رشته دودویی رمزشده مان را کمینه کند.

به صورت دقیق تر فرض کنید می خواهیم درخت رمزگذاری ارائه دهیم که متن \(s\) را به دنباله دودویی \(p\) تبدیل کند به طوریکه طول \(p\) کمینه شود. فرض کنید از حرف \(i\) ام \(c_i\) تا در رشته \(s\) داشته باشیم. حالا طول \(p\) برابر با \(\sum h_i \times c_i\) خواهد بود پس می خواهیم این مقدار را کمینه کنیم.

فرض کنید درخت رمزگذاری مورد نظر \(T\) باشد. به چند نکته زیر توجه کنید :

• اگر حرف ها را بر اساس تعداد تکرار های آن ها (\(c_i\)) از کم به زیاد مرتب کنیم \(h_i\) ها از زیاد به کم مرتب خواهند بود. (در غیر اینصورت می توانیم راس متناظر به دو حرف را جا به جا کنیم تا طول \(p\) کم تر شود).
• تمام برگ ها برادر دارند (مگر اینکه تنها یک برگ داشته باشیم). در غیراینصورت می توان آن برگ را حدف کرد حرفی که به آن نسبت داده شده را به پدرش نسبت دهیم. در اینصورت طول \(p\) کم می شود.
• اگر دو برگ \(a\) و \(b\) در یک ارتفاع باشند می توان حرف هایی که به \(a,b\) نسبت داده شده را با هم جا به جا کرد و تغییری در اندازه \(p\) ایجاد نمی شود.

پس می توان نتیجه گرفت اگر دو حرفی که تعداد تکرار های آن ها کمینه است را \(x,y\) در نظر بگیریم آن ها در پایین ترین ارتفاع درخت هستند.همچنین می توان راس های نسبت داده شده به آن ها را طوری جا به جا کرد که آن دو برادر باشند!

پس حالت بهینه ای وجود دارد که برگ های متناظر با \(x,y\) دو برادر در پایین ترین ارتفاع درخت باشند. فرض کنید ارتفاع راس متناظر با \(x,y\) برابر با \(h\) باشد. از آنجایی که رشته دودویی متناظر به \(x,y\) تنها در یک رقم آخر (یعنی رقم \(h\) ام) با هم تفاوت دارند پس می توان فهمید رقم \(h\) ام آن دو روی هم \(c_x + c_y\) بار آمده است.

در ادامه می توان دو حرف \(x\) و \(y\) را حذف کرد و یک حرف جدید مثلا \(z\) تعریف کرد که به جای \(x,y\) می آید و قرار است راس متناظر با \(z\) همان پدر مشترک \(x,y\) باشد پس حالا از تعداد حروف الفبا ای که داشتیم یکی کم کردیم و می توان مسئله را بازگشتی برای آن ها حل کرد. اگر جواب مسئله جدید (مینیمم طول \(p\)) را \(ans ^ {\prime}\) فرض کنید جواب مسئله فعلی ما \(ans = ans ^ {\prime} + c_x + c_y\) خواهد بود.

همچنین می توانید ببینید که درخت بهینه \(T\) که به صورت وجودی آن را فرض کرده بودیم در طی مراحل الگوریتم خود به خود ساخته خواهد شد!

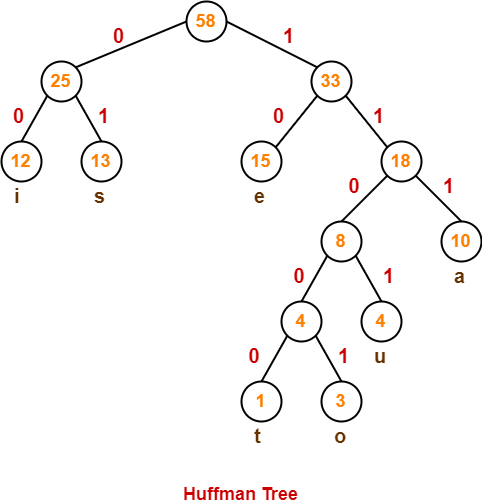
پس الگوریتم به اینصورت است که در هر مرحله دو حرفی که کمترین تعداد تکرار را دارند (مثلا \(x,y\)) با هم ترکیب کرده و یک حرف جدید جایگزین آن می کنیم که تعداد تکرار های آن \(c_x + c_y\) است و سپس \(c_x + c_y\) را به جواب اضافه می کنیم.

پیاده سازی این الگوریتم را می توانید در ادامه ببینید.

typedef pair<int, int> pii;

const int maxn = 1e5 + 10;

vector<int> Tree[maxn]; // bache haye har raas dar derakht ramz gozari

int c[maxn]; // tedad tekrar haye har harf
int Counter; // kamtarin id raasi ke nadarim ra negah midarad
priority_queue<pii, vector<pii>, greater<pii> > pq; // yek heap minimum

int main(){
    int n; // tedad horoof alephba
    cin >> n;
    for(int i = 0; i < n; i++){
          cin >> c[i];
           pq.push({c[i], i});
    }
    Counter = n;
    int ans = 0;
    while(pq.size() > 1){
       int x = pq.top().second, y = pq.top().second;
       pq.pop(), pq.pop();
       int z = Counter;
       Counter++;
       Tree[z].push_back(x);
       Tree[z].push_back(y);
       c[z] = c[x] + c[y];
       ans+= c[x] + c[y];
       pq.push({c[z], z});
    }
    // dar inja ans kamine tool p mibashad va dar Tree yek derakht ramzgozari behine sakhtim.
}