تورنومنت¶
تعریف 3.2.1 (تورنمنت)¶
تورنمنت، گراف ساده و کاملی است که یالهای آن جهتدار شدهاند (شکل 1 تورنمنتی با 5 راس میباشد).
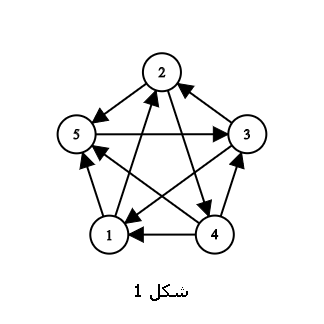
یک تورنمنت \(n\) راسی میتواند مدلی برای مسابقات بین \(n\) تیم باشد به طوری که از راس 1 به راس 2 یال جهتدار است اگر و تنها اگر تیم 1 از تیم 2 برده باشد (مانند شکل 1).
شاه در تورنمنتها¶
تعریف 3.2.2 (شاه)¶
شاه، راسی درتورنمنت است که به تمام راسهای تورنمنت مسیری جهتدار به طول حداکثر 2 دارد. به عنوان مثال راس 3، یک شاه در شکل 1 میباشد.
قضیه 3.2.3¶
صورت قضیه : هر تورنمنت حداقل یک شاه دارد.
اثبات قضیه : فرض کنید \(v\) راسی با درجه خروجی \(\Delta^{+}\) در تورنمنت باشد، یعنی راسی باشد که بیشنیه درجه خروجی را دارد. اگر راسی مانند \(u\) وجود داشتهباشد که نتوان از \(v\) به آن با مسیری با طول حداکثر 2 برسیم، در این صورت \(u\) باید به \(v\) و تمام راسیهای مانند \(w\) که \((v,w) \in E\) ، یال جهتدار داشتهباشد (شکل 2) که در این صورت \(d^{+}(u) \geq \Delta^{+}+1\) که با بیشینه بودن درجه خروجی \(v\) در تناقض است. پس درنتیجه راسی وجود ندارد که از \(v\) نتوان با حداکثر دو یال به آن رسید و \(v\) ، شاه است.
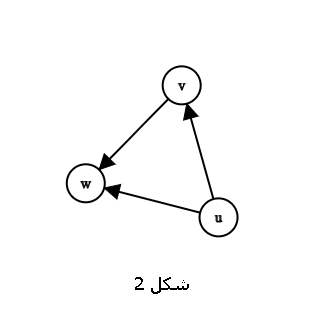
قضیه 3.2.3 مانند این میباشد که به عنوان مثال در یک تورنمنت مسابقات، فردی مانند \(v\) وجود دارد که به ازای هر نفر مانند \(u\) یا آن را برده است یا شخصی را برده که \(u\) را برده است.
مسیر همیلتونی در تورنمنت¶
تعریف 3.2.4(مسیر همیلتونی در گراف جهتدار)¶
یک مسیر همیلتونی در گراف جهتدار، مسیر جهتداری است که از تمام راسها بگذرد.
قضیه 3.2.5¶
صورت قضیه : هر تورنمنت دارای حداقل یک مسیر همیلتونی است.
اثبات قضیه : فرض کنید راسهای \(a_1\) تا \(a_k\) بلندترین مسیر جهتدار در تورنمنت را تشکیل دهند (شکل 3).
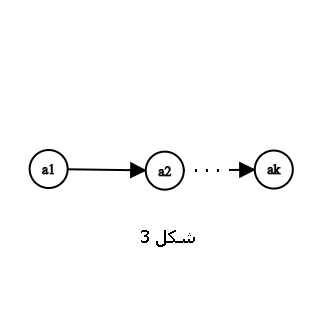
اگر \(k = n\) که حکم اثبات میشود، در غیر این صورت راسی مانند \(v\) وجود دارد که در این مسیر نمیباشد. از \(v\) به \(a_1\) و از \(a_k\) به \(v\) نمیتواند یال جهتدار باشد (چرا؟)، پس فرض کنید \(a_i\) راسی با کوچکترین \(i\) بین تمام راسها از \(a_1\) تا \(a_k\) باشد که \(v\) به آنها یال دارد. در این صورت راسهای \(a_1,...,a_{i-1},v,a_i,...,a_k\) مسیری با طول \(k+1\) تشکیل میدهند، در صورتی که طول بلندترین مسیر برابر \(k\) میباشد. در نتیجه \(k = n\) و \(a_1\) تا \(a_k\) تشکیل یک مسیر همیلتونی میدهند.
