کاربرد ها¶

گراف جهت دار و دوبخشی¶

در این بخش می بینیم که دو مفهوم گراف دوبخشی و جهت دار قابل تبدیل به یکدیگر هستند و بسته به اینکه کدام یک شهود بهتری برای حل مسئله به ما می دهند می توانیم از یکی از آن دو استفاده کنیم.

ماتریس مجاورت یک گراف دوبخشی و جهت دار را در نظر بگیرید. هر دو ماتریسی \(n*n\) هستند که در خانه ها 0,1 قرار دارد. (لزوما ماتریس متقارن نیست)

حالا برای تبدیل گراف جهت دار به دوبخشی کافیست ماتریس مجاورت گراف جهت دار که آن را \(M\) می نامیم در نظر بگیرید و گراف دو بخشی رسم کنید که ماتریس مجاورت آن \(M\) باشد. تبدیل گراف دوبخشی به جهت دار نیز مشابه است. اگر بخواهیم شهودی تر به مطلب نگاه کنیم هر یال \(ab\) در گراف جهت دار معادل یک یال بین راس \(a\) از بخش سمت چپ و راس \(b\) از بخش سمت راست است. یعنی بخش سمت چپ نماینده خروجی ها و بخش سمت راست نماینده ورودی ها است.

حالا یک تطابق در گرافی دوبخشی را در نظر بگیرید. اگر گراف دوبخشی را به گراف جهت دار تبدیل کنیم تطابق ما به چه چیزی تبدیل خواهد شد؟

تعدادی دور و مسیر جهت دار! زیرا که در گراف دوبخشی از هر راس حداکثر یک یال مجاور انتخاب شده است این موضوع در گراف جهت دار به این معنی است که هر راس حداکثر یک ورودی و حداکثر یک خروجی دارد.

افراز dag به مسیر ها¶

یک گراف جهت دار بدون دور داریم. مینیمم \(x\) که می توان این گراف را به \(x\) مسیر جهت دار افراز کرد چند است؟

توجه کنید که اگر در این افراز بهینه تعداد یال های مسیر ها \(y\) باشد آنگاه \(x+y=n\) پس برای مینیمم کردن \(x\) کافی است \(y\) را ماکسیمم کنیم. گراف جهت دار را به دوبخشی تبدیل کنید. حالا \(y\) برابر است با ماکسیمم تطابق این گراف دوبخشی.‌ (چرا؟)

افراز گراف جهت دار به دور ها¶

فرض کنید در یک گراف جهت دار می خواهیم یک روش برای افراز کردن این گراف به دور ها پیدا کنیم.

ابتدا گراف را به فرم دوبخشی در بیاورید. گفتیم یک تطابق به معنای افراز به دور ها و مسیر ها است. می توانید به راحتی نتیجه گیری کنید که یک تطابق کامل به ما یک افراز به دور ها را ارائه می دهد. پس کافیست یک تطابق کامل در گراف دوبخشی پیدا کنیم.

گراف 2k منتظم و افراز به دور ها¶

این بار موضوع بحث ما گرافی بی جهت است. مشابه مسئله بالا تصور کنید گرافی بی جهت مثل \(G\) داریم و می دانیم \(2k\) منتظم است. می خواهیم اثبات کنیم یک روش برای افراز این گراف به دور ها وجود دارد.

اولین ایده این است که به ازای هر یال \(G\) مثل \(ab\) در یک گراف جهت دار دو یال \(ab, ba\) را قرار دهیم. سپس مشابه مسئله بالا ابتدا گراف جهت دار را به فرم دوبخشی در بیاوریم و سپس تلاش کنیم تطابقی کامل پیدا کنیم.

مشکلی که در این راه به وجود می آید این است که در این افراز ممکن است دور هایی به طول 2 (که همان تک یال می باشند) به وجود بیاید که این موضوع برای ما مطلوب نیست.

برای اینکه این مشکل به وجود نیاید تور اویلری گراف را در نظر بگیرید و هر یال را در جهتی که تور اویلری آن را می پیماید جهت دار کنید. (اگر گراف چندین مولفه همبندی داشت این کار را برای هر کدام از مولفه ها انجام می دهیم). حالا گراف حاصل گرافی جهت دار است که در هر راس آن درجه ورودی و خروجی برابر با \(k\) می باشد. حالا اگر این گراف را به فرم دوبخشی در بیاوریم هر راس آن درجه \(k\) خواهد داشت.

طبق قضیه ای که قبلا ثابت کردیم گراف دوبخشی \(k\) منتظم تطابق کامل دارد پس در این گراف جهت دار هم روشی برای افراز به دور ها وجود دارد.

دنباله درجه ای تورنومنت و تطابق¶

فرض کنید دنباله \(d_1,d_2,...d_n\) داده شده است و می دانیم \(\sum\limits_{i=1}^{n} d_i = {n \choose 2}\).می خواهیم بررسی کنید آیا تورنومنتی وجود دارد درجه خروجی هر راس مثل \(u\) برابر با \(d_u\) باشد؟

گرافی دوبخشی بسازید. بخش سمت راست \(n\) راس دارد و سمت چپ \(n \choose 2\) راس دارد و هر کدام از راس های بخش سمت چپ به نشانه یک یال از تورنومنت می باشد. راسی که به نشانه یال \(ab\) است را به راس \(a\) و راس \(b\) از بخش سمت راست متصل کنید. حالا یک زیرمجموعه از یال ها انتخاب کنید که درجه هر راس سمت چپ برابر با 1 و درجه راس \(u\) از بخش سمت راست برابر با \(d_u\) باشد. (شبیه تطابقی که در بخش تعمیم هال بررسی کردیم).

به طور شهودی این هر راس سمت چپ مثل راسی که به نشانه \(ab\) است باید یکی از دو راس \(a\) یا \(b\) را انتخاب کند. اگر \(a\) را انتخاب کند یعنی قرار است در تورنومنت یال بین راس \(a,b\) از \(a\) به \(b\) جهت دار شده باشد و بالعکس. همچنین قرار است درجه خروجی راس \(u\) در تورنومنت برابر با \(d_u\) باشد پس هر راس \(u\) از بخش سمت چپ باید توسط دقیقا \(d_u\) راس از بخش سمت چپ انتخاب شده باشد!

پس طبق مطالبی که در بخش تعمیم هال بررسی کردیم شرط لازم و کافی برای وجود داشتن چنین تورنومنتی این است که به ازای هر زیرمجموعه از راس های سمت چپ مثل \(S\) اگر اجتماع مجاور های آن در بخش سمت راست \(P\) باشد آنگاه : \(|S| \leq \sum\limits_{u \in P} d_u\) از آنجایی که می توانیم بدون تغییر دادن سمت راست نامساوی، سمت چپ را تا \(|P| \choose 2\) زیاد کنیم (چرا؟) پس می توانیم شرط را به این صورت نیز بنویسیم :

\(\forall_{P \subseteq \{1,2,...,n\}} {|P| \choose 2} \leq \sum\limits_{u \in P} d_u\)

حالا از آنجایی که در سمت چپ نامساوی تنها تعداد اعضای مجموعه مهم است نه خود مجموعه پس کافیست شرط را به ازای کمترین \(d_u\) ها بررسی کنیم. به عبارتی با فرض \(d_1 \leq d_2 \leq ... d_n\) شرط زیر لازم و کافی می باشد :

\(\forall_{1 \leq k \leq n} {k \choose 2} \leq \sum\limits_{i=1}^{k} d_i\)

راس های ثابت در تطابق دو بخشی¶

یک گراف دوبخشی داریم. به ازای تطابق \(M\) هر راس \(u\) که مجاور یکی از یال های \(M\) باشد را حاضر در \(M\) می گوییم. حالا شما باید به ازای تمام راس ها مثل \(u\) بگویید آیا تطابقی ماکسیممی وجود دارد که \(u\) در این تطابق حاضر نباشد؟

ابتدا یک تطابق ماکسیمم دلخواه مثل \(M\) را در نظر بگیرید. حالا به ازای تمام راس هایی که در \(M\) حاضر نیستند جواب را می دانیم. و می خواهیم به ازای هر راس حاضر در \(M\) مثل \(u\) جواب را بیابیم. فرض کنید تطابق ماکسیممی مثل \(M^{\prime}\) وجود دارد که \(u\) در آن حاضر نیست. حالا فرض کنید تفاضل متقارن \(M\) و \(M^{\prime}\) برابر با \(H\) باشد. در اینصورت \(H\) باید شامل تعدادی دور و مسیر زوج باشد همچنین \(u\) باید ابتدای یکی از این مسیر های زوج باشد(چرا؟)!

پس نتیجه می گیریم به ازای هر راس \(u\) که عضو تطابق \(M\) هست می توانیم تطابقی پیدا کنیم که \(u\) در آن حاضر نباشد اگر و فقط اگر مسیری متناوب از راسی آزاد (راسی که در تطابق \(M\) نیامده است) به \(u\) وجود داشته باشد دقت کنید از آنجایی که این مسیر افزوده مسیر افزایشی نیست پس دو سر مسیر در یک بخش از گراف دوبخشی ما قرار دارند.

تا اینجای کار از دوبخشی بودن گراف استفاده ای نکردیم (تمام حکم هایی که بیان شد برای هر گرافی صدق می کند). اما حالا برای پیدا کردن یک تطابق ماکسیمم و راس هایی که شروع مسیر متناوب هستند باید از دوبخشی بودن گراف استفاده کنیم.

ابتدا با الگوریتمی که در بخش 12.2 ارائه دادیم تطابق ماکسیمم \(M\) را پیدا کنید.

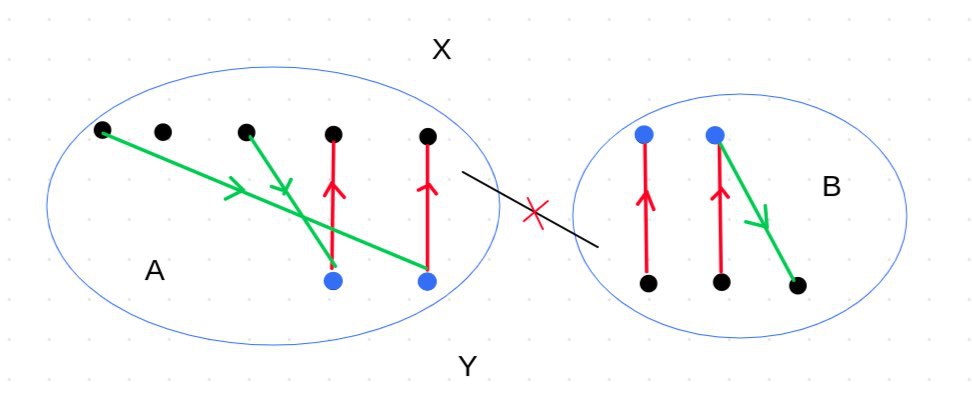
حالا فرض کنید دو بخش گراف \(X\) و \(Y\) باشند و ما می خواهیم به ازای بخش \(X\) مسئله را حل کنیم یال های گراف را جهت دهی می کنیم به این صورت که یال هایی که عضو \(M\) هستند را از \(Y\) به \(X\) و یال هایی که عضو \(M\) نیستد را از \(X\) به \(Y\) جهت دهی می کنیم. می توانید ببینید که یک هر مسیر متناوب با شروع از یک راس \(X\) در واقع معادل با مسیری در گراف جهت دهی شده ما است که باید از یکی از راس های آزاد \(X\) شروع شود.

پس کافی است گراف را همانطور که گفتیم جهت دهی کنید و سپس از هر راس آزاد \(X\) الگوریتم dfs را اجرا کنید و بررسی کنید به کدام راس ها می رسیم. در نهایت تمامی راس های \(X\) که توانستیم به آن ها برسیم در یک مسیر متناوب قرار دارند. همانطور که گفتیم این موضوع به این معناست که به ازای هر کدام از آن راس ها تطابق ماکسیممی وجود دارد که آن راس در تطابق حاضر نباشد.

مشابها می توانیم مسئله را برای بخش \(Y\) هم حل کنیم.

پیدا کردن یک مینیمم پوشش راسی در گراف دو بخشی¶

در بخش 12.3 فهمیدیم که در گراف دوبخشی اندازه مینیمم پوشش راسی برابر است با اندازه ماکسیمم تطابق. در این قسمت یاد میگیریم چگونه با داشتن ماکسیمم تطابق، مینیمم پوشش راسی را پیدا کنیم.

ابتدا یال های ماکسیمم تطابق را در نظر بگیرید و آن را \(M\) بنامید. از آنجایی که به ازای هر یال تطابق یکی از دو سر آن باید در پوشش راسی آمده باشد پس از هر یال دقیقا یکی از دو سر آن در مینیمم پوشش راسی آمده است (چرا؟). پس کافیست به ازای یال \(M\) تصمیم بگیریم که راسی که عضو بخش اول گراف است را در پوشش راسی بگذاریم یا راسی که در بخش دوم گراف است.

دو بخش گراف را \(X\) و \(Y\) بنامید. مجموعه یال هایی از \(M\) که برای آن ها بخش \(X\) را انتخاب می کنیم \(MX\) بنامید و مجموعه یال هایی از \(M\) که برای آن ها بخش \(Y\) را انتخاب می کنیم \(MY\) بنامید. حالا می خواهیم \(MX, MY\) را مشخص کنیم.

مشابه بخش قبل یال های گراف دوبخشی را جهت دهی می کنیم به اینصورت که یال های عضو \(M\) را از بخش \(Y\) به \(X\) و یال هایی که عضو \(M\) نیستند را از \(X\) به \(Y\) جهت دهی می کنیم. حالا از تمامی راس های بخش \(X\) که در تطابق حاضر نیستند dfs بزنید. تمام راس هایی که آن ها را می بینیم \(A\) و بقیه را \(B\) بنامیم. واضح است که بین \(X \cap A\) و \(Y \cap B\) یال نیست (در غیر اینصورت مجموعه \(A\) تغییر می کرد). پس می توان تمام راس هایی که در \(Y \cap A\) و \(X \cap B\) هستند را در پوشش راسی انتخاب کرد. از آنجایی که در هیچ یک از این دو مجموعه راس آزاد نداریم (به دلیل اینکه \(M\) ماکسیمم است پس مسیر افزایشی نداریم) می توان نتیجه گرفت حرفمان معادل این است که تمام یال هایی که در dfs دیده می شوند را \(MY\) قرار دهیم و باقی را \(MX\) قرار دهیم. یعنی \(MX = M - MY\).