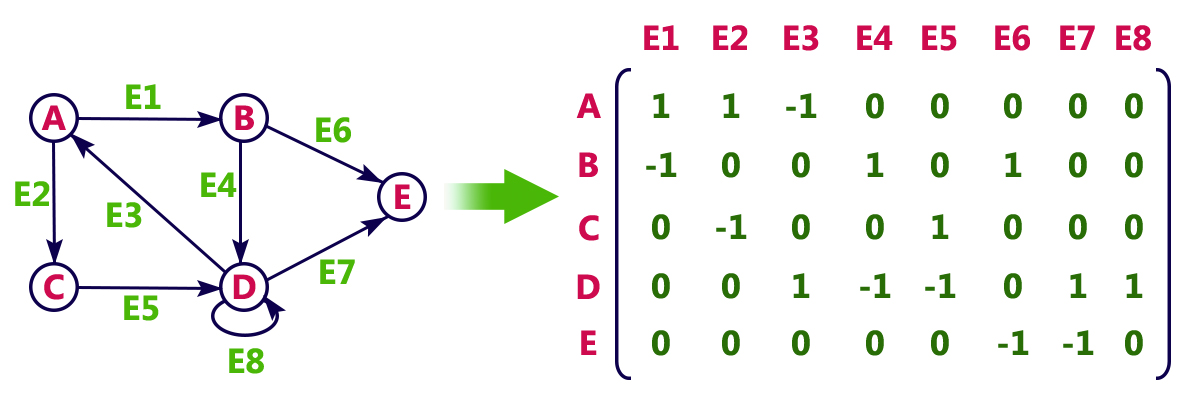
ماتریس وقوع¶

ماتریس وقوع¶

در گراف های ساده به ماتریس n × m که در آن \(a_{ij}\) یک است اگر راس i یک سر یال j باشد و صفر است اگر راس i یک سر یال j نباشد. تمامی درایه های این ماتریس صفر یا یک است.

اگر یال چندگانه هم وجود داشته باشد ماتریس وقوع مشکلی پیدا نخواهد کرد چرا که فقط به تعداد ستون اضافه می شود و فرقی در ساختار و کلیت ماتریس وقوع نمی کند. اما اگر طوقه داشته باشیم قضیه کمی فرق می کند چرا که راسی که طوقه دارد بجای عدد یک، عدد دو می گیرد، یعنی \(a_{ij}\) مقدار دو می گیرد اگر راس i طوقه j را داشته باشد.

در گراف های جهت دار ساختار متفاوتی در ماتریس وقوع پدیدار می شود. به این صورت که \(a_{ij}\) مقدار یک می گیرد اگر یال j از راس i خارج شود یا یال j طوقه باشد، مقدار منفی یک می گیرد اگر یال j به راس i وارد شود و در صورتی که هیچ کدام از حالات بالا نباشد مقدار صفر را به خود می گیرد. مجموع مقادیر ماتریس وقوع در یک گراف جهت دار تعداد طوقه ها را به ما می دهد.