تطابق در گراف دوبخشی¶

الگوریتم¶

در این الگوریتم از تطابق خالی شروع می‌کنیم و تا زمانی که مسیری افزایشی در گراف وجود داشت تطابق را بزرگ‌تر می‌کنیم. به راحتی قابل مشاهده است که در این صورت ماکسیمم بودن تطابق نهایی ما بدیهی است. برای پیدا کردن مسیر افزایشیبه این صورت عمل میکنیم:

فرض کنید گراف ما شامل دو بخش \(n_1\) راسی و \(n_2\) راسی باشد. به ازای \(v = 1 ... n_1\) در گراف حال حاضرمان به دنبال مسیر افزایشی می‌گردیم. در مرحله \(i\) ام می‌توان ادعا کرد تطابقی که بین \(i\) راس بخش اول و بقیه رئوس بخش دوم است ماکسیمم است، در نتیجه در آخر نیز تطابق ما ماکسیمم خواهد بود. پیاده‌سازی آن به شکل زیر است:

const int N = 2e3 + 5;
int n1, n2, m, k, match[N];
vector <int> adj[N];
bool mark[N];

bool try_kuhn(int u){
    mark[u] = true;
    for(auto v: adj[u])
        if(match[v] == -1 || (!mark[match[v]] && try_kuhn(match[v]))){
            match[v] = u;
            return true;
        }
    return false;
}

void read_input(){
    cin >> n1 >> n2 >> m;
    for(int i = 0; i < m; i++){
        int u, v;
        cin >> u >> v;
        adj[--u].push_back(--v);
    }
}

void calc(){
    memset(match, -1, sizeof match);
    for(int u = 0; u < n1; u++){
        memset(mark, false, sizeof mark);
        k += try_kuhn(u);
    }
}

void write_output(){
    cout << k << endl;
    for(int u = 0; u < n2; u++)
        if (match[u] != -1)
            cout << match[u] + 1 << ' ' << u + 1 << endl;
}

int main() {
    read_input();
    calc();
    write_output();
    return 0;
}

در الگوریتم ذکر شده به ازای هر راس از بخش بالا، \(O(m)\) گام انجام می‌شود، پس پیچیدگی زمانی آن برابر \(O(nm)\) است. البته یک نوع پیاده‌سازی دیگر همین الگوریتم نیز وجود دارد که سرعت آن حداقل دوبرابر سریع‌تر از الگوریتم بالا است (چرا؟):

const int N = 2e3 + 5;
int n1, n2, m, k, match[N];
vector <int> adj[N];
bool mark[N];

bool try_kuhn(int u){
    mark[u] = true;
    for(auto v: adj[u])
        if (match[v] == -1 || (!mark[match[v]] && try_kuhn(match[v]))) {
            match[v] = u;
            return true;
        }
    return false;
}

void read_input(){
    cin >> n1 >> n2 >> m;
    for(int i = 0; i < m; i++){
        int u, v;
        cin >> u >> v;
        adj[--u].push_back(--v);
    }
}

void calc(){
    memset(match, -1, sizeof match);
    while(true){
        bool flag = false;
        memset(mark, false, sizeof mark);
        for(int u = 0; u < n1; u++)
            if (!mark[u])
                k += try_kuhn(u);
        if (!flag)
            break;
    }
}

void write_output(){
    cout << k << endl;
    for (int u = 0; u < n2; u++)
        if (match[u] != -1)
            cout << match[u] + 1 << ' ' << u + 1 << endl;
}

int main(){
    read_input();
    calc();
    write_output();
    return 0;
}

قضیه هال¶

این قضیه شرط لازم و کافی دیگری برای ماکسیمم بودن یک تطابق در یک گراف دوبخشی را بیان می‌کند که اولین بار توسط فیلیپ هال مطرح شد و به قضیه ازدواج معروف است. این قضیه به شرح زیر است:

فرض کنید \(X\) مجموعه‌ای از رئوس بخش اول یک گراف دوبخشی باشد. مجموعه \(X\) در گراف تطابق کامل دارد، اگر و تنها اگر به ازای هر زیرمجموعه از آن مثل \(S\) و مجموعه همسایه‌های خارج \(X\) آن‌ها در گراف به نام \(T\)، داشته باشیم \(|S| \leq |T|\).

لازم بودن شرط بالا بدیهی است (در غیر این صورت تعداد رئوس مجاور یک مجموعه برای تطابق دادنشان کافی نخواهد بود). برای اثبات کافی بودن نیز از برهان خلف استفاده می‌کنیم و فرض می‌کنیم گرافی با چنین خاصیتی باشد که تطابق کامل نداشته باشد؛

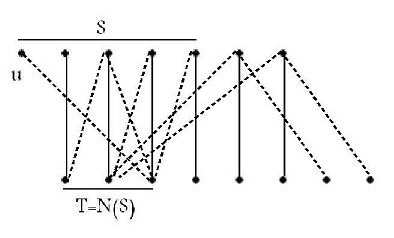
یک تطابق ماکسیمم را درنظر می‌گیریم و راس دلخواهی مثل \(u\) که غیراشباع است را درنظر می‌گیریم (حتماً وجود دارد!). از آنجا که این راس با کسی منطبق نشده، راس منطبق یک راس دلخواه مجاور آن را درنظر میگیریم. این دو راس طبق فرض مسئله یک راس مجاور دیگر دارند که یا منطبق نشده (که در این صورت مسیر افزایشی داریم) و یا منطبق شده که راس منطبق آن را نیز به این دو راس اضافه می‌کنیم. این کار را تا جای ممکن ادامه می‌دهیم و از آنجا که تعداد رئوس مجاور \(X\) حداقل اندازه خودشان است، در آخر به مرحله‌ای میرسیم که مجموعه حال حاضرمان یک راس مجاور دارند که اشباع نشده که در این صورت مسیر افزایشی داریم که این با ماکسیمم بودن تطابقمان در تناقض است.

تطابق در گراف دوبخشی k منتظم¶

طبق قضیه هال می‌توان اثبات کرد که گراف دوبخشی k منتظم تطابق کامل دارد. برای اثبات این موضوع نیز کافیست اثبات کنیم که شرط هال برای آن برقرار است؛

مجموعه‌ای از رئوس بخش اول گراف مثل \(S\) را درنظر بگیرید و همسایه‌های آن‌ها در بخش دوم را \(T\) بنامید. اثبات می‌کنیم \(|S| \leq |T|\). می‌دانیم مجموع یال‌های بین دو بخش برابر \(x = |S| \times k\) است. از این رابطه می‌توان نتیجه گرفت \(|T| \geq (x \div k) = |S|\).

پس حکم حال در گراف ما برقرار است و قطعاً در گراف ما تطابقی کامل یافت می‌شود.

تعمیم قضیه هال¶

یک گراف دوبخشی به نام \(G\) داریم و می‌خواهیم تعدادی از یال‌های آن را برداریم، طوری که درجه هر راس بخش اول مثل \(u\) برابر \(a_u\) و درجه هر راس بخش دوم حداکثر یک شود. برای حل این مسئله گراف \(G'\) را به گونه‌ای میسازیم که در آن تطابق کامل از بخش اول به دوم وجود دارد، اگر و تنها اگر در گراف \(G\) چنین مجموعه یال‌هایی وجود داشته باشد؛

گراف \(G'\) را بدین گونه می‌سازیم که به جای هر راس \(u\) در گراف از بخش اول، یک مجموعه \(a_u\) تایی از رئوس می‌سازیم (که کپی هایی از راس \(u\) هستند) و به ازای هر یال گراف مثل \((u, v)\)، تمام مجموعه راس \(u\) را به راس \(v\) متصل می‌کنیم. گراف حاصل دوبخشی است (چرا؟) اگر شرط هال در آن برقرار باشد یعنی تطابق کامل دارد که در این صورت به ازای هر یال بین مجموعه رئوس راس \(u\) و راس \(v\) در گراف، یال \((u, v)\) را در گراف \(G\) برمی‌داریم که بدیهی است که در این صورت به مجموعه یال‌های دلخواهمان می‌رسیم. در صورتی هم که گراف \(G'\) تطابقی کامل نداشته باشد به همین شکل می‌توان نتیجه گرفت که در گراف \(G\) نیز چنین مجموعه‌ای وجود ندارد (به صورت برعکس عمل میکنیم).

فرایند چک کردن شرط هال در گراف \(G^{\prime}\) را در نظر بگیرید.به ازای هر زیرمجموعه \(S\) که از بخش اول گراف \(G ^ {\prime}\) و مجموعه همسایه های آن \(T\) است، چک می کنیم که \(|S| \leq |T|\) برقرار باشد. حالا می توان توجه کرد که به ازای هر راس \(u\) اگر تعدادی از کپی های \(u\) در \(S\) آمده باشد ولی همه آن ها نیامده باشند می توان همه را به مجموعه \(S\) اضافه کرد در اینصورت \(T\) تغییری نخواهد کرد و تنها \(S\) زیاد می شود. پس می توان فقط \(S\) هایی را چک کرد که به ازای هر \(u\) یا تمام کپی های \(u\) آمده اند یا هیچکدام نیامده اند.

با کمی تفکر نتیجه می گیریم که طبق حرف های بالا می توان روی گراف \(G\) این شرط لازم و کافی را پیدا کرد : \(\forall_{S} \sum\limits_{i \in S} a_i \leq |T|\)

که \(S\) هر زیرمجموعه ای از راس های بخش اول گراف است و \(T\) اجتماع همسایه های \(S\) است.