برش ها و همبندی¶
همبندی یکی از مباحث پر کاربرد در گراف است که در برنامه نویسی هم مورد استفاده قرار می گیرد. بدون مقدمه سازی بیشتر به سمت تعاریف و قضایا می رویم تا بیشتر با همبندی آشنا شویم.
همبندی¶
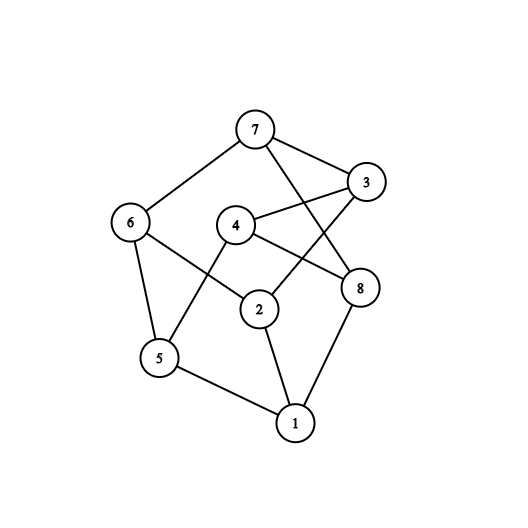
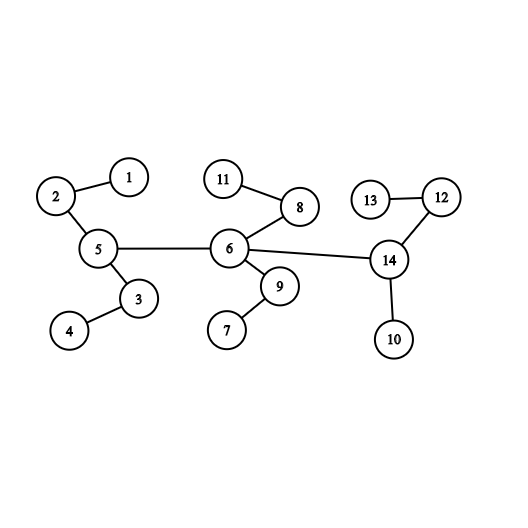
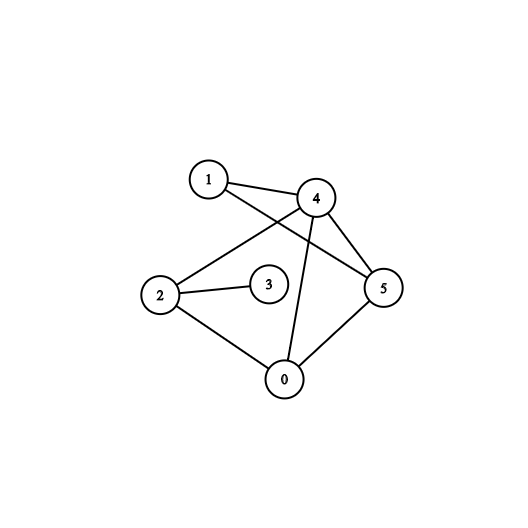
همبند بودن یک گراف به این معناست که بین هر دو راس گراف مسیر وجود داشته باشد.
مولفه همبندی¶
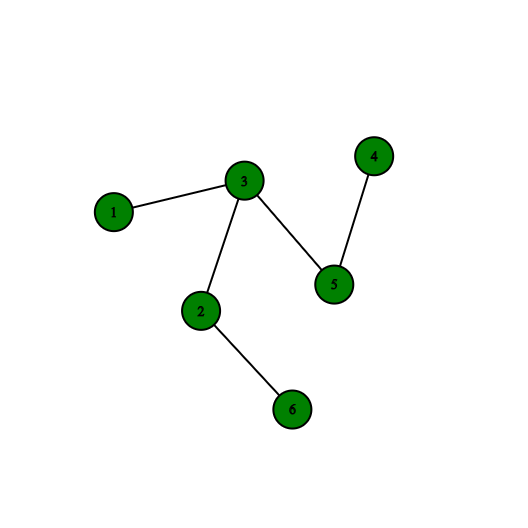
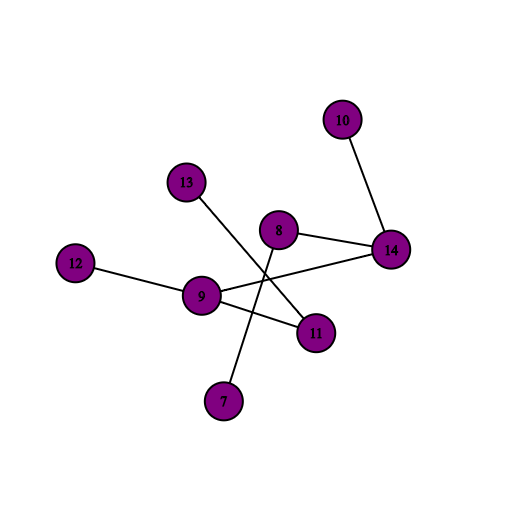
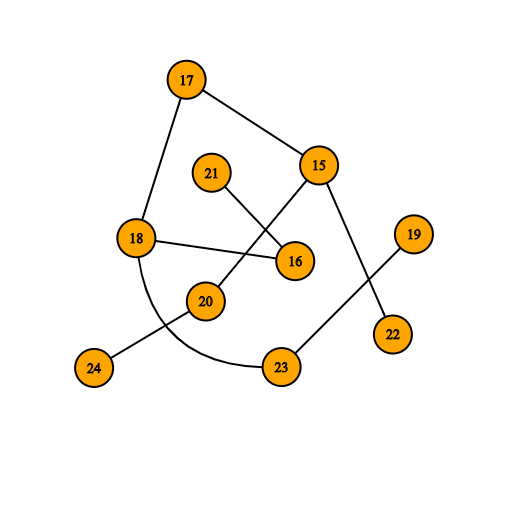
به هر قسمت همبند گراف مولفه همبندی می گویند. هر گرافی که بیش از یک مولفه داشته باشد، گراف ناهمبند گویند. برای مثال در یک جنگل به هر درخت موجود مولفه می گویند و تعداد مولفه های جنگل برابر تعداد درخت های موجود در آن است. در جنگل زیر هر مولفه با رنگ متفاوت نشان داده شده است.
همبندی در گراف های جهت دار¶
ضعیفاً همبند¶
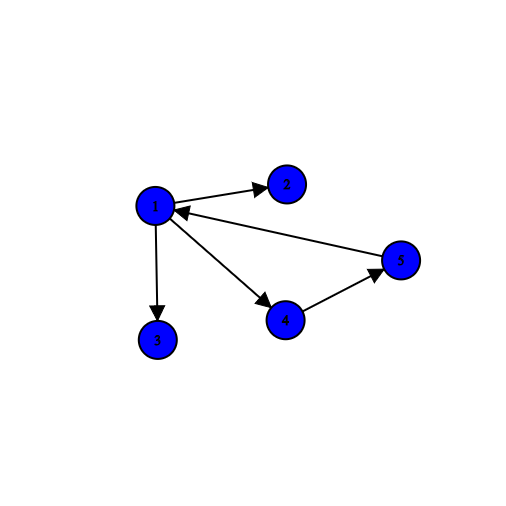
یال های گراف جهت دار را با یال های بی جهت عوض می کنیم در این صورت اگر گراف همبند باشد گوییم گراف اصلی (با یال های جهت دار) ضعیفاً همبند است.
قویاً همبند¶
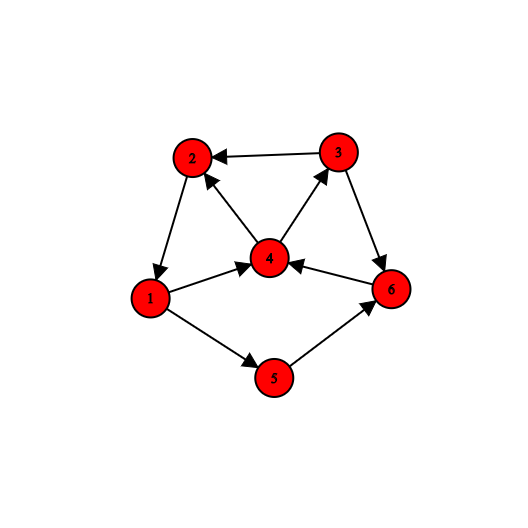
به گراف جهت داری که بین هر دو راس u و v آن، مسیری جهت دار از u به v و مسیری جهت دار از v به u وجود داشته باشد، قویاً همبند گویند.
برای حل مسائل \(2-SAT\) از الگوریتم های موجود برای پیدا کردن اجزای قویاً همبند استفاده می شود.
مولفه قوی¶
مولفه قوی زیر گراف های قویاً همبند ماکسیمال گراف هستند.
برش ها¶
راس برشی¶
به راسی برشی گفته می شود که بعد از حذف آن از گراف به تعداد مولفه های آن اضافه شود.
یال برشی¶
یال برشی به یالی گفته می شود که با حذف آن تعداد مولفه های همبندی افزایش پیدا کند. همچنین به آن یال برشی نیز گفته می شود. یال uv که در دوری از گراف وجود دارد نمی تواند برشی باشد، چرا که با حذف آن دو راس u و v همچنان یه گشت به هم دارند پس مولفه ای به گراف اضافه نمی شود.
