دنباله درجه ای¶
گرافی \(n\) راسی مانند \(G\) را در نظر بگیرید.
فرض کنید درجه راس \(i\) را به صورت \(d_{i}\) نشان دهیم. آنگاه به دنباله \(d_{1}, d_{2}, ..., d_{n}\) دنباله درجه‌ای گراف \(G\) می‌گوییم.
دنباله گرافیک¶
به دنباله‌ی \(d_{1}, d_{2}, ..., d_{n}\) یک دنباله گرافیک گوییم، اگر گرافی ساده \(n\) راسی مانند \(G\) وجود داشته باشد، که دنباله درجه راس های آن، برابر با دنباله فوق باشد.
الگوریتم هاول حکیمی¶
این الگوریتم برای تشخیص دنباله های گرافیک به کار می رود. این الگوریتم یک الگوریتم حریصانه است و هر بار، راس بزرگترین درجه را به راس های با درجه های بزرگ بعدی وصل می کند و اگر در یک مرحله، مجبور شدیم به یک راس درجه صفر یال وصل کنیم، یعنی دنباله ما گرافیک نیست. درستی این الگوریتم حریصانه معادل این قضیه است که یک دنباله مرتب شده \(d_{1}, d_{2}, ..., d_{n}\) که در آن \(d_{1} \ge d_{2} \ge ... \ge d_{n}\) گرافیک است اگر و تنها اگر \(d_{2} - 1 , d_{3} -1 , ... d_{d_1+1} -1, d_{d_1+2}, ... , d_{n}\) گرافیک باشد.
جابه جایی دوتایی¶
در راستای اثبات قضیه هاول حکیمی، تعریف می‌کنیم عملیات جابه‌جایی دوتایی را بین 4 راس \(a, b, c, d\) به این‌صورت که فرض کنید بین \(a, b\) و \(c, d\) یال باشد و بین \(a, c\) و \(b, c\) یالی نباشد.
در این‌صورت، یال های \(a, b\) و \(c, d\) را از گراف حذف می‌کنیم و یال های \(a, c\) و \(b, c\) را اضافه می‌کنیم. برای درک بهتر، به شکل زیر توجه کنید.
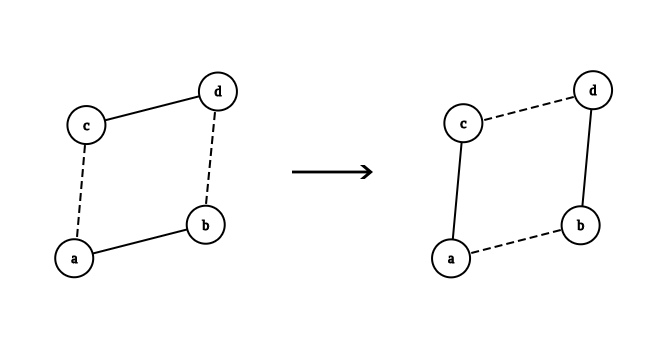
نکته مهم این تبدیل این است که با اجرای آن، دنباله درجه ای گراف بدون تغییر باقی می ماند.
اثبات قضیه¶
یک سمت این قضیه، بدیهی است چون اگر دنباله \(d_{2} - 1 , d_{3} -1 , ... d_{d_1+1} -1, d_{d_1+2}, ... , d_{n}\) گرافیک باشد با در نظر گرفتن گراف متناظر آن و اضافه کردن یک راس، می توان نشان داد که دنباله اصلی نیز گرافیک بوده است.
حال سمت دیگر را اثبات می کنیم. طبق فرض دنباله اصلی گرافیک است و ما باید ثابت کنیم که دنباله \(d_{2} - 1 , d_{3} -1 , ... d_{d_1+1} -1, d_{d_1+2}, ... , d_{n}\) نیز گرافیک است. بین تمام گراف هایی که دنباله درجه ای برابر با دنباله ما دارند، آن را در نظر بگیرید که راس شماره یک به بیشترین تعداد راس از \(v_{2} , v_{3} , ... v_{d_1+1}\) که از این به بعد آن ها را رئوس خوب و بقیه را رئوس بد می نامیم وصل باشد. اگر راس شماره یک به تمامی رئوس خوب وصل باشد، با حذف آن گراف مورد نظر ساخته می شود و حکم برقرار است. در غیر این صورت، یکی از رئوس خوب که به راس یک متصل نیست را در نظر بگیرید و یک راس بد که به راس یک متصل هست را نیز در نظر بگیرید. اگر راس خوب همسایه ای داشته باشد که مجاور راس بد نباشد، می توان روی این چهار راس یک عملیات جابه جایی دوتایی اجرا کرد و به این ترتیب تعداد رئوس خوب مجاور راس یک یک واحد زیاد می شود که با فرض اکسترمال در تناقض است. در غیر این صورت، تمام مجاور های راس خوب مجاور راس بد نیز هستند و علاوه بر آن راس بد مجاور راس شماره یک نیز هست. پس درجه راس بد از راس خوب اکیدا بیشتر است که با فرض مرتب شده بودن درجات در تناقض است. بنابراین حکم ثابت شد و یعنی دنباله خواسته شده درجه ای است.
این کتاب توسط مشارکت کنندگان شاززز به وجود آمده است.
این کتاب عمومی است و تحت پروانه cc-by-sa در دسترس است.
آخرین به روز رسانی در ژوئن 09, 2022.
