برش کمینه و جریان بیشینه¶

برابری با برش کمینه¶

همان گراف مساله بالا را در نظر بگیرید. می‌خواهیم مجموعه ای از یال ها را حذف کنیم که راس مبدا به مقصد مسیر جهتدار نداشته باشد. هدف این است که جمع ظرفیت یال های حذف شده کمینه شود. به این مساله، مساله برش کمینه می‌گویند. در ادامه ثابت می‌کنیم که در هر گراف جریان بیشینه با برش کمینه برابر است.

اثبات¶

ابتدا واضح است که اندازه هر برشی از اندازه هر جریانی بیشتر است. زیرا حذف هر یال حداکثر به اندازه ظرفیتش از میزان جریان کم می کند و تا زمانی که جریان وجود داشته باشد ما به یک برش نرسیده ایم. برای اثبات اینکه جریان بیشینه با برش کمینه برابر است یک جریان بیشینه را در نظر می گیریم و یک برش به اندازه آن به دست می آوریم.

جریان بیشینه را در نظر بگیرید. یک مسیر افزایش دهنده مسیری است با این شرط که اگر از یک یال در جهت خودش در مسیر استفاده کرده ایم، نباید از تمام ظرفیتش استفاده شده باشد و اگر در جهت برعکس از آن استفاده می کنیم، باید حتما جریانی از آن رد شده باشد، برای مثال مسیر زیر یک مسیر افزایش دهنده است:

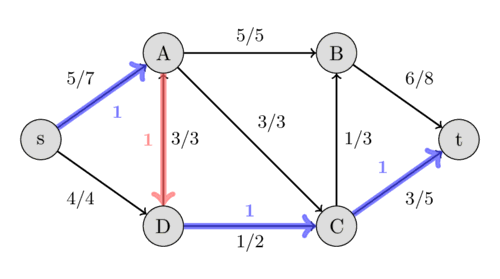
در یک جریان بیشینه، مسیر افزایش دهنده از مبدا به مقصد وجود ندارد. زیرا اگر وجود داشته باشد می توان جریان گذرنده را بیشتر کرد، کافیست که جریان یال هایی که در جهت مسیر هستند (یال های آبی) را یک واحد زیاد و جریان بقیه یال ها را یک واحد کم کنیم. با این کار جریان یک واحد بیشتر می شود.

حال برای پیدا کردن یک برش به اندازه جریان بیشینه = f، می توانید رئوسی را در نظر بگیرید که از راس مبدا به آن مسیر افزایش دهنده وجود دارد. طبق مطلب بالا راس مقصد در این مجموعه نیست. جریان ورودی این مجموعه ۰ است زیرا اگر یالی از خارج این مجموعه وجود داشته باشد که از آن جریان گذشته باشد و به داخل این مجموعه باشد، آنگاه راس خارج مجموعه این یال نیز باید داخل این مجموعه باشد چون مسیر افزایش دهنده به آن وجود دارد. جمع جریان ورودی و خروجی هر مجموعه برابر جمع جریان ورودی و خروجی هر راس در آن مجموعه است. و جمع جریان ورودی و خروجی هر راس دقیقا ۰ است به جز راس ورودی و خروجی. راس ورودی f واحد جریان خروجی دارد پس جمع جریان ورودی و خروجی مجموعه ای که ما در نظر گرفتیم دقیقا f است و چون جریان ورودی این مجموعه ۰ است، در نتیجه جریان خروجی این مجموعه f است. یال های خروجی این مجموعه را در نظر بگیرید، همه ظرفیتشان تماما تکمیل است (وگرنه مسیر افزایش دهنده به رئوس خروجی این یال ها وجود داشت) و جمع ظرفیت هایشان دقیقا f است. این یال ها را قطع کنید، دیگر مسیری از مبدا به بیرون این مجموعه و در نتیجه به مقصد وجود ندارد. پس ما برشی به اندازه f یعنی اندازه بزرگترین جریان بیشینه پیدا کردیم. پس جریان بیشینه برابر برش کمینه است.

الگوریتم فورد فلکرسون برای جریان بیشینه¶

سعی می کنیم که یک مسیر افزایش دهنده از مبدا به مقصد پیدا کنیم و به کمک آن یک واحد به جریان اضافه کنیم. آن قدر این کار را ادامه می دهیم تا دیگر مسیر افزایش دهنده وجود ندارد. یک جریان به دست می آید که برشی به اندازه آن وجود دارد. و چون می دانیم که همه برش ها بزرگتر مساوی همه جریان ها هستند، جریانی که پیدا کرده ایم قطعا جریان بیشینه است.

قطعه کد زیر پیاده سازی این الگوریتم است. برای سادگی کار، به جای این که برای پیدا کردن مسیر حالت های در جهت و در خلاف جهت را جداگانه بررسی کنیم، به ازای هر یال یک یال در خلاف جهت آن و با وزن ۰ قرار می دهیم. هر گاه که از یک یال جریانی گذراندیم، ظرفیت خودش را کم می کنیم و به ظرفیت یال دوگان آن یال اضافه می کنیم.

int cnt, head[M], pre[M], cap[M], to[M], from[M];
int n,m;

void add(int u, int v, int w){
    // ezafe kardane yale asli
    from[cnt] = u;
    to[cnt] = v;
    pre[cnt] = head[u];
    cap[cnt] = w;
    head[u] = cnt++;
    // ezafe kardane yale dogaan
    from[cnt] = v;
    to[cnt] = u;
    pre[cnt] = head[v];
    cap[cnt] = 0;
    head[v] = cnt++;
}

int tnod = 0;
bitset <M> mark;

// say mikonim ke masir afzaayesh dahande peydaa konim
int dfs(int u, int mn){
    mark[u] = 1;
    if(u == tnod)return mn;
    // yal haye ras u dar yek link list rikhte shode and.
    for (int i = head[u]; i != -1; i = pre[i]){
        // agar yale hadaf zarfiat nadasht bikhiaale aan mishavim
        if (cap[i] == 0 || mark[to[i]]) continue;
        // say mikonim ke jaryani be maghsad peyda konim
        int s = dfs(to[i], min(mn,cap[i]));
        // agar s = 0 nabashad, masir afzayesh dahande i vojood darad ke
        // kam zarfiat tarin yale aan s vahed zarfiat darad
        if (s){
            // az zarfiate yal s vahed kam mikonim
            cap[i] -= s;
            // be zarfiate yaale dogan s vahed ezafe mikonim
            cap[i^1] += s;
            // elam mikonim ke masir s vahedi peyda shode ast
            return s;
        }
    }
    // masiri peyda nakardim
    return 0;
}

int maxflow(){
    int flow = 0;
    while(1){
        mark &= 0;
        int s = dfs(0, inf);
        // agar masiri peyda nashode bood flow = maxflow
        if (!s) return flow;
        flow += s;
    }
}

در این الگوریتم برای پیدا کردن مسیر افزایش دهنده از الگوریتم DFS استفاده کرده ایم. این الگوریتم در هر مرحله حداقل یک واحد به جریان موجود اضافه می کند و چون زمان DFS خطی است این الگوریتم پیچیدگی زمانی \(O(ef)\) دارد که e تعداد یال ها و f مقدار بیشینه جریان است. اگر به جای الگوریتم DFS از الگوریتم BFS استفاده می کردیم کران \(O(ve^2)\) نیز ثابت شده بود که به اثبات آن نمی پردازیم.

پیدا کردن عدد همبندی راسی و یالی¶

به کمک الگوریتم جریان بیشینه می توان عدد همبندی راسی و یالی را در زمان چند جمله ای به دست آورد.

برای به دست آوردن عدد همبندی یالی، به ازای هر یال دو یال جهت دار با وزن ۱ در خلاف جهت هم بین این دو راس اضافه می کنیم. سپس بین هر دو راس جریان بیشینه را پیدا می کنیم که برابر برش کمینه نیز هست. با توجه به این که برش کمینه هر دو جهت یال را قطع نمی کند، برش کمینه این گراف با گراف بی جهت برابر است. و هر برش دو راس را ناهمبند می کند پس از عدد همبندی یالی گراف بیشتر است و چون کمینه یال های لازم برای ناهمبند کردن یک گراف دو راس را از هم جدا می کند کمینه این برش ها همان عدد همبندی یالی گراف است. پیچیدگی زمانی این الگوریتم \(O(v^3e)\) است زیرا جواب از تعداد راس ها کمتر است.

برای به دست آوردن عدد همبندی راسی گراف، یک گراف جدید می سازیم که به ازای هر راس دو راس دارد. یک راس ورودی و یک راس خروجی. به ازای هر یال نیز دو یال اضافه می کنیم. از راس های ورودی متناظر به راس های خروجی متناظر. برای هر راس نیز از ورودی به خروجی یال می کشیم. یال های متناظر با یال ها ظرفیت بینهایت و یال های درون هر راس ظرفیت ۱ دارد. برای این که به دست بیاوریم که چه میزان راس مورد نیاز است حذف شود تا دو راس مورد نظر ناهمبند شوند، می توان برش کمینه بین این دو راس را در گراف به دست آورد. برای هر دو راس این مقدار را محاسبه می کنیم و عدد همبندی راسی به دست می آید. پیچیدگی زمانی این الگوریتم \(O(v^3e)\) است زیرا جواب از تعداد راس ها کمتر است.