گراف مسطح¶
گراف مسطح گرافی است که می توان آن را روی صفحه رسم کرد بدون آن که یال هایش از روی هم دیگر بگذرند. گراف های زیر مسطح هستند:
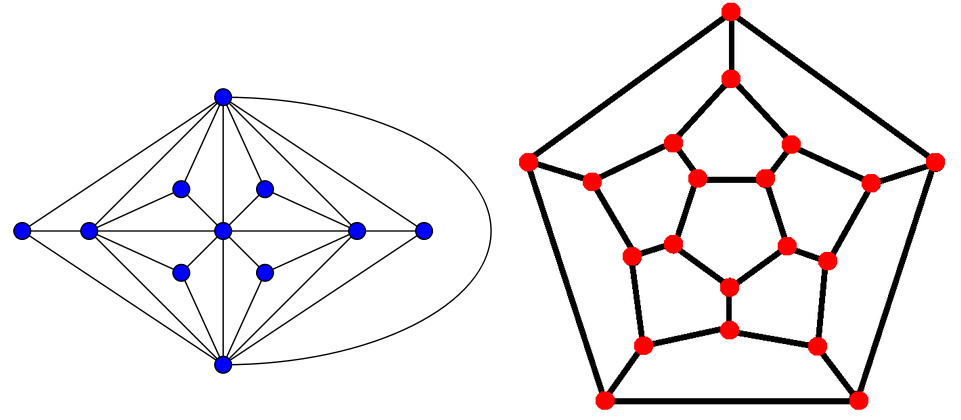
گرافی که نتوان روی صفحه به این صورت رسم کرد، گراف غیر مسطح است. برای مثال گراف کامل پنج راسی غیر مسطح است. ( امتحان کنید :) )
رسم گراف مسطح روی کره¶
یک گراف را می توان روی کره رسم کرد به صورتی که یال های آن یکدیگر را قطع نکنند اگر و تنها اگر مسطح باشد. برای اثبات از تبدیل زیر استفاده می کنیم.
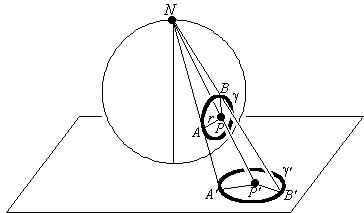
یک کره را روی صفحه قرار دهید و قطب مخالف نقطه مماس به صفحه را در نظر بگیرید. (نقطه N) هر خطی که شامل این نقطه باشد دقیقا یک نقطه از صفحه و یک نقطه از کره را می پوشاند. حال برای اثبات قضیه یک گراف مسطح را روی صفحه در نظر بگیرید و آن را روی کره رسم کنید. به این صورت که به ازای هر نقطه از صفحه خط از N به آن را رسم کنید و نقطه معادل آن در کره را به دست آورید. حال اگر آن نقطه از صفحه یک راس بود، روی کره راس، اگر یال بود نقطه ای از یال و اگر ناحیه بود نقطه ای از ناحیه روی آن بگذارید. به این صورت یک رسم از گراف روی کره به دست می آید. می توان دید که یال ها بیوستگی خود را از دست نمی دهند و بدیهیست که یکدیگر را قطع نمی کنند.
برای سمت دیگر قضیه نیز به طور مشابه عمل می کنیم. اما دقت می کنیم که نقطه N روی راس یا یال نباشد. ناحیه ای که آن نقطه روی آن است تبدیل به ناحیه نامتناهی که گراف را احاطه کرده می شود.
قضیه اویلر¶
قضیه اویلر رابطه ای برای به دست آوردن تعداد ناحیه های تشکیل شده در یک گراف مسطح است. این قضیه بیان می کند که:
که در آن f تعداد ناحیه ها، e تعداد یال ها، t تعداد مولفه ها و n تعداد رئوس است. به طور خاص در گراف همبند، داریم:
اثبات¶
اثبات این قضیه اصلا پیچیده نیست، بنابراین خوب است که ابتدا خودتان به آن فکر کنید. اگر گراف یک جنگل باشد، حکم برقرار است چون یک ناحیه وجود دارد و داریم \(e = n - t\) اما اگر جنگل نباشد، یکی از یال هایی که درون دور آمده و غیر برشی است را از گراف حذف می کنیم. تعداد رئوس و مولفه ها ثابت می ماند اما تعداد نواحی و تعداد یال ها دقیقا یک واحد کم می شود. پس اگر حکم در گراف جدید درست باشد، در گراف قبلی نیز درست بوده است. آن قدر این کار را ادامه می دهیم تا به یک جنگل برسیم. چون در جنگل حکم برقرار است، در تمام گراف های این بین از جمله گراف ابتدایی نیز برقرار بوده است.
گراف دوگان¶
گراف دوگان یک گراف مسطح، گرافی است که به این صورت به دست می آید: در هر ناحیه یک راس قرار دهید، سپس بین راس های متناظر با ناحیه های مجاور یال قرار دهید. مانند شکل زیر:
توجه کنید که گراف دوگان نیز مسطح است. گراف دوگان در حل مسائل مربوط به گراف مسطح می تواند مفید باشد.
گراف اشباع¶
گراف اشباع یک گراف مسطح ساده است که نمی توان به آن یال اضافه کرد و باز هم مسطح ساده بماند. یک گراف که بیش از دو راس دارد اشباع است اگر و تنها اگر هر ناحیه سه ضلع داشته باشد یا به عبارت دیگر گراف دوگان آن سه منتظم باشد. در یک گراف اشباع داریم:
که اگر آن را درون رابطه اویلر قرار دهیم ( گراف اشباع به وضوح همبند است ) به دست می آید:
که ثابت می کند که در هر گراف ساده مسطح
