تطابق در گراف های عام¶
در فصل های قبل شرط لازم و کافی برای وجود داشتن تطابق کامل در گراف های دوبخشی را بررسی کردیم. در این قسمت وجود تطابق کامل در هر گرافی را بررسی خواهیم کرد.
قضیه تات¶
به ازای هر زیر مجموعه \(S\) از راس ها (که می تواند تهی نیز باشد) فرض کنید \(O(S)\) برابر با تعداد مولفه های همبندی با اندازه فرد باشد در صورتیکه رئوس \(S\) را از گراف حذف کرده باشیم.
قضیه تات بیان می کند شرط زیر لازم و کافی می باشد :
\(\forall_S : |S| \geq O(S)\)
شرط تات به وضوح برای وجود تطابق کامل لازم است. برای اثبات به ازای یک مجموعه \(S\) داشته باشیم \(|S| < O(S)\). در اینصورت برای وجود تطابق کامل باید از هر مولفه فرد که در \(O(S)\) شمردیم باید یک راس به راسی در \(S\) مطابق شده باشد. از آنجایی که گفتیم \(|S| < O(S)\) پس پیدا کردن تطابق کامل امکان پذیر نیست.
برای اثبات کافی بودن شرط از اکسترمال استفاده می کنیم. یعنی با استفاده از برهان خلف فرض کنید گراف \(G\) تطابق کامل ندارد و شرط تات در آن صدق می کند. توجه کنید که با اضافه کردن یال به گراف \(G\) شرط تات برقرار می ماند (چرا؟). پس ایده کلی ما به این صورت است که تا زمانی که در گرافمان تطابق کامل به وجود نیاید یک یال که در آن حضور ندارد را به آن اضافه خواهیم کرد. در نهایت به گراف ماکسیمال \(H\) می رسیم که :
- شرط تات در آن صدق می کند.
- در آن تطابق کامل وجود ندارد.
- به ازای هر یال \(uv\) که در \(H\) نیست در صورتی که آن را به \(H\) اضافه کنیم تطابق کامل به وجود خواهد آمد.
حالا هدف ما این است که ثابت کنیم گراف \(H\) همین حالا هم تطابق کامل دارد (در اینصورت با فرض خلف به تناقض می خوریم و مسئله اثبات می شود).
ابتدا توجه کنید که برقرار بودن شرط تات به ازای \(S = \phi\) به ما نتیجه می دهد که \(H\) دارای هیچ مولفه همبندی با فرد راس نیست در نتیجه تعداد راس های گراف زوج است.
- گلابی : راس های \(a,b,c,d\) به طوریکه \(ab,ac\) یال‌های گراف باشند ولی \(bc,ad\) یال‌های گراف نباشند.
- سیب : راس های \(a,b,c\) به طوریکه \(ab,ac\) یال‌های گراف باشند ولی \(bc\) یال گراف نباشد.
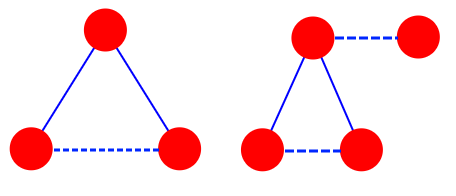
ادعا می کنیم اگر بتوانیم در \(H\) یک گلابی پیدا کنیم می توانیم ثابت کنیم در \(H\) تطابق کامل وجود دارد. پس یک گلابی دلخواه را در نظر بگیرید و راس های آن را \(a,b,c,d\) مطابق تعریف در نظر بگیرید.
اگر به \(H\) یال \(ad\) را اضافه کنید در آن تطابق \(M1\) وجود خواهد داشت که شامل \(ad\) است.
اگر به \(H\) یال \(bc\) را اضافه کنید در آن تطابق \(M2\) وجود خواهد داشت که شامل \(bc\) است.
حالا \(M = M1 \Delta M2\) را در نظر بگیرید. طبق مطالب گفته شده در قسمت های قبل یال های \(M\) به صورت تعدادی دور می باشد.
اگر یال \(ad\) و \(bc\) در دو دور متفاوت باشند¶
آنگاه از دوری که \(ad\) درون آن است یال های \(M2\) و از دوری که \(bc\) درون آن است یال های \(M1\) را انتخاب کنید (از بقیه دور ها به صورت دلخواه یال های \(M1\) یا \(M2\) را انتخاب کنید و یال هایی که در \(M1 \cap M2\) هستند را نیز انتخاب کنید). در اینصورت در \(H\) یک تطابق کامل خواهیم داشت!
اگر یال \(ad\) و \(bc\) در یک دور باشند¶
در ابتدا باید بگوییم که این دور زوج است. حالا چون \(b,c\) یکی از یال های دور است \(b,c\) دو راس متوالی در دور هستند پس در صورتیکه به ازای دقیقا یکی از یال های \(ab\) یا \(ac\) اتفاق زیر می افتد :
اگر راس های دو سر یال را از گراف حذف کنیم دور ما تبدیل به دو مسیر زوج راسی خواهد شد.
بدون کم شدن از کلیت مسئله فرض کنید این یال \(ab\) باشد. حالا یال \(ab\) را برای تطابق انتخاب کنید. و سپس \(a,b\) را از گراف حذف کنید و یال های دو مسیر زوج راسی به وجود آمده را یکی در میان برای تطابق انتخاب کنید. در اینصورت تمام راس های دور ما توسط یال های انتخاب شده پوشش داده می شوند. مشابه بالا از بقیه دور ها به صورت دلخواه یال های \(M1\) یا \(M2\) را انتخاب کنید و یال هایی که در \(M1 \cap M2\) هستند را نیز انتخاب کنید. در اینصورت در \(H\) یک تطابق کامل خواهیم داشت!
اگر گلابی نداشتیم چه؟¶
در دو قسمت بالا ثابت کردیم اگر در گراف \(H\) گلابی داشتیم آنگاه \(H\) دارای یک تطابق کامل است. حالا باید حالاتی که در \(H\) گلابی وجود ندارد را هم در نظر بگیریم.
مجموعه \(C\) را شامل تمام راس های \(H\) در نظر بگیرید که به همه راس های دیگر یال دارند (درجه آن ها \(n-1\) است).
حالا اگر \(C\) تمام راس های \(H\) را شامل شود به این معنی است که \(H\) یک خوشه (و دارای زوج راس) است.پس به وضوح در آن تطابق کامل وجود دارد.
پس گراف \(W = H-C\) را در نظر بگیرید. در \(W\) به ازای هر راس مثل \(u\) راسی مثل \(v\) وجود دارد که بین \(uv\) یالی نیست (چرا؟). پس اگر بتوانیم در \(W\) یک سیب پیدا کنیم آنگاه می توانیم یک گلابی هم پیدا کنیم(زیرا تنها کافیست به ازای راس \(a\) در سیب راس \(d\) را طوری بیابیم که بین \(a,d\) یال نباشد).
پس اگر در \(W\) سیب وجود داشته باشد مسئله حل می شود. پس فرض کنید در \(W\) سیب وجود ندارد. در اینصورت به ازای هر \(a,b,c\) دلخواه که \(ab,ac\) یال گراف هستند، \(bc\) هم باید یال این گراف باشد. یک راس دلخواه مثل \(u\) را در نظر بگیرید و مجموعه خود \(u\) و راس های مجاور آن را \(A\) در نظر بگیرید. بین هر دو راس در \(A\) باید یال باشد(چرا؟) همچنین هیچ راسی خارج از \(A\) نیست که به \(A\) یال داشته باشد(چرا؟). پس می توان نتیجه گرفت که هر مولفه همبندی در \(W\) یک خوشه است. در هر خوشه راس ها را به صورت دلخواه تطابق دهید. از هر خوشه فرد دقیقا یک راس اضافه می ماند. از آنجایی که به ازای \(S = C\) شرط تات برقرار است پس می توان تمام راس های اضافه مانده در \(W\) را به راس های \(C\) تطابق داد. در نهایت کل راس های اضافه مانده در \(C\) را (که یک خوشه زوج راسی هستند) را به صورت دلخواه تطابق می دهیم. پس در نهایت یک تطابق کامل در \(H\) پیدا کردیم.
حالت کلی تر تطابق یا k-factor¶
طبق تعریف یک تطابق کامل در گراف \(G\) به معنی یک زیرمجموعه از یال های گراف مثل \(M\) است که در \(M\) درجه هر راس دقیقا 1 باشد.
حالا می خواهیم این تعریف را تعمیم دهیم. فرض کنید \(a_1,a_2,...,a_n\) داده شده است و ما باید بفهمیم آیا یک زیرمجموعه از یال های گراف مثل \(M\) وجود دارد که در آن درجه هر راس \(u\) برابر با \(a_u\) شود؟
در نگاه اول این مسئله بسیار کلی تر و سخت تر از تطابق است ولی در این بخش می خواهیم آن را با استفاده از تطابق حل کنیم.
یک ایده اشتباه¶
احتمالا اولین ایده ای که به ذهن می رسد این است که راس \(u\) را دقیقا \(a_u\) بار کپی کنیم سپس به ازای هر یال \(uv\) در \(G\) بین تمام کپی های \(u,v\) یال قرار دهیم. سپس بررسی کنیم که در گراف جدید تطابق کامل وجود دارد یا خیر.
این ایده بسیار شبیه به آن چیزی است که قبلا در فصل تطابق دوبخشی بررسی کردیم اما یک اشتباه بسیار ریز دارد. مشکل این است که ممکن است همزمان از چند تا از یال های بین \(u,v\) در تطابق استفاده کنیم و این باعث می شود که از یک یال چند بار استفاده کنیم که مطلوب مسئله نیست.
حل درست¶
فرض کنید \(d_u\) درجه راس \(u\) باشد. از گراف \(G\) گراف \(G^{\prime}\) را به اینصورت می سازیم :
به ازای هر راس \(u\) یک گراف دوبخشی کامل قرار می دهیم! به صورتی که بخش اول آن دارای \(d_u - a_u\) راس قرار داشته باشد و در بخش دوم آن \(d_u\) راس قرار داشته باشد. به گراف دوبخشی متناظر با راس \(u\) ، \(B_u\) گوییم. سپس یال های گراف \(G\) را به ترتیبی دلخواه در نظر بگیرید و متناظر آن را (به صورتی که خواهیم گفت) به گراف \(G^{\prime}\) اضافه کنید. فرض کنید \(i\) امین یالی که بررسی می کنیم \(uv\) باشد و قبل از آن \(c1\) تا از یال های مجاور \(u\) و \(c2\) تا از یال های مجاور \(v\) را بررسی کرده ایم. حالا متناظر یال \(uv\) برابر خواهد بود با یالی که بین دو راس زیر است :
- راس \(c1\) ام بخش دوم گراف \(B_u\)
- راس \(c2\) ام بخش دوم گراف \(B_v\)
حالا ادعا می کنیم وجود داشتن زیرمجموعه \(M\) از یال ها که شرط مسئله را برآورده کند معادل است با وجود داشتن یک تطابق کامل در گراف \(G^{\prime}\)!
توجه کنید که در این گراف هر یال در گراف اصلی دقیقا یک یال متناظر دارد پس مشکل قبل (چند بار استفاده کردن از یک یال) پیش نمی آید. اثبات کامل درستی قضیه بالا به عهده خواننده واگذار می شود.
این کتاب توسط مشارکت کنندگان شاززز به وجود آمده است.
این کتاب عمومی است و تحت پروانه cc-by-sa در دسترس است.
آخرین به روز رسانی در ژوئن 09, 2022.
