آشنایی¶

تعریف¶

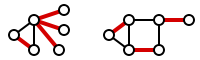
تطابق مجموعه‌ای از یال‌هاست که هیچ‌دوتایی از آنها باهم راس مشترک ندارند.

به زبان ریاضی، اگر گراف را \(G\) و مجموعه یال‌های آن را \(E\) درنظر بگیریم، به زیرمجموعه‌ای از \(E\) که هیچ‌یک از دو عضو آن راس مشترکی در \(G\) ندارند، تطابق یا مجموعه‌ ناوابسته‌ یال‌ها می‌گویند و آن را با \(M\) نشان می‌دهند.

به راسی که در یکی از دو انتهای یال‌های تطابق گراف \(G\) واقع شده باشد، راس اشباع (منطبق شده) و در غیر این صورت راس غیراشباع (منطبق نشده) می‌گویند.

تطابق ماکسیمال و ماکسیمم¶

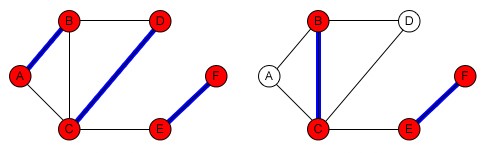
تطابق ماکسیمال یک تطابق در \(G\) است، به صورتی که هر یال دیگری که در تطابق نیامده باشد را که به آن اضافه کنیم، گراف به وجود آمده خاصیت تطابق بودن خود را از دست بدهد. به عبارتی دیگر، تطابق \(M\) زمانی ماکسیمال است که هر یال \(G\) حداقل با یکی از یال‌های آن تقاطع داشته باشد.

تطابق ماکسیمم تطابقی است که بیشترین تعداد یال‌های \(G\) را دارد. بنابراین می‌توان نتیجه گرفت هر تطابق ماکسیمم، یک تطابق ماکسیمال است، ولی هر تطابق ماکسیمال لزوما یک تطابق ماکسیمم نیست.

تطابق کامل نیز تطابقی است که در آن همه راس‌ها اشباع هستند (در اصل تعداد یال‌های آن برابر \(|G| / 2\) است). همچنین به راحتی می‌توان دید که تطابق ماکسیمال حداقل برابر نصف تطابق ماکسیمم است.

مسیر متناوب و افزایشی¶

مسیر متناوب، مسیری است که یال‌های آن یکی در میان در میان یال‌های تطابق و خارج از یال‌های تطابق است.

مسیر افزایشی، مسیری متناوب است که راس‌های اول و آخر آن غیراشباع هستند و در تطابق وجود ندارند.

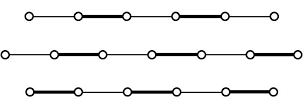
یک تطابق ماکسیمم است، اگر و تنها اگر مسیر افزایشی نداشته باشد که این نتیجه‌گیری به قضیه‌ی برژ نیز معروف است.

برای اثبات این که تطابق ماکسیمم مسیر افزایشی ندارد می توانیم با فرض خلف یک مسیر افزایشی در نظر بگیریم. چون مسیر افزایشی یک مسیر متناوب است و راس اول و آخر آن درون تطابق نیستند می توان یال های تطابق که در این مسیر هستند را از تطابق حذف کرد و یال های دیگر این مسیر را به جای آن ها به تطابق اضافه کرد. چون راس اول و آخر درون تطابق نیستند یال های خارج از تطابق در هر مسیر افزایشی یکی بیشتر از یال های درون تطابق است. پس به اندازه تطابق یک واحد اضافه می شود و تطابق بزرگتری ساخته می شود، که با فرض ماکسیمم بودن تطابق اولیه در تناقض است. پس تطابق بیشینه، هیچ مسیر افزایشی ندارد.

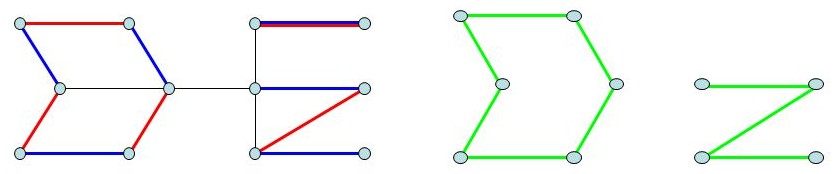
اثبات عکس این قضیه یعنی اگر تطابقی مسیر افزایشی نداشته باشد آنگاه تطابق ماکسیمم است نیز به روش برهان خلف قابل انجام است: فرض کنید تطابق \(M'\) تطابقی ماکسیمال بدون مسیر افزایشی و تطابق \(M\) تطابق بیشینه است. در این صورت گراف \(M \Delta M'\) را درنظر بگیرید. درجه هر راس در آن حداکثر برابر دو است. پس این گراف از تعدادی دور و مسیر یکی‌درمیان تشکیل می‌شود. در دور‌ها و مسیرهای زوج، تعداد یال‌های هر دو تطابق باهم برابر است. در مسیرهای فرد نیز حتما اولین و آخرین یال از \(M\) است، زیرا در غیر این صورت می‌توانستیم به جای یال‌های \(M\) در مسیر از یال‌های \(M'\) استفاده کنیم و اندازه تطابق را افزایش دهیم. پس اگر مسیر فردی داشته باشیم یعنی حداقل یک مسیر افزایشی داریم که این تناقض است. پس نتیجه میگیریم که مسیر فردی نداریم و \(|M| = |M'|\).

پوشش راسی و یالی¶

به مجموعه‌ای (پوششی) از رئوس که هر یال حداقل یکی از دو سرش در این مجموعه آمده باشد، پوشش راسی می‌گوییم.

به مجموعه‌ای (پوششی) از یال‌ها که هر راس حداقل یکی از یال‌های مجاورش در این مجموعه آمده باشد، پوشش یالی می‌گوییم.

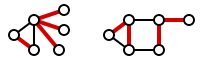
به پوشش راسی با مینیمم تعداد راس، مینیمم پوشش راسی و به پوشش یالی با مینیمم تعداد یال، مینیمم پوشش یالی می‌گوییم.