مولفه‌های قویا همبند¶

تعریف 3.4.1 (جفت راس قویا همبند)¶

در گراف جهت‌­دار به جفت راس \((v, u)\) قویا همبند گوییم اگر و تنها اگر مسیری از \(v\) به \(u\) و مسیری از \(u\) به \(v\) وجود داشته باشد.

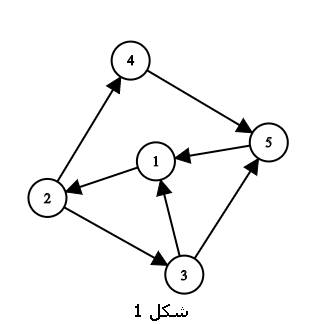
به عنوان مثال در شکل 1، راس­‌های 2 و 4 یک جفت راس قویا همبند هستند.

تعریف 3.4.2 (گراف قویا همبند)¶

گراف قویا همبند، گراف جهت­‌داری است که هر جفت راس آن قویا همبند باشند (شکل 1).

تعریف 3.4.3 (مولفه قویا همبند (strongly connected component یا به اختصار scc))¶

یک مولفه قویا همبند در گراف جهت­‌دار \(G\) ، زیرمجموعه­‌ای از رئوس \(G\) می­‌باشند که در زیرگراف القایی آن­‌ها تشکیل یک گراف قویا همبند را دهد و همچنین ماکسیمال باشد، یعنی نتوان راس دیگری به آن اضافه کرد.

لم 3.4.4¶

صورت لم: هر راس \(v\) در گراف جهت­‌دار \(G\) ، تنها در یک مولفه قویا همبند یکتا قرار دارد.

اثبات: از برهان خلف استفاده می­‌کنیم. فرض کنید که \(v\) در دو مولفه قویا همبند \(H\) و \(L\) قرار دارد و \(u\) راسی در \(L\) باشد که در \(H\) قرار ندارد. چون \(u\) و \(v\) در یک مولفه قویا همبند قرار دارند، در نتیجه از هر راسی در \(H\) می­‌توان با مسیری به \(v\) آمد و سپس با مسیری به \(u\) رفت و همچنین با مسیری از \(u\) به \(v\) آمد و با مسیری به هر راس دلخواه در \(H\) رفت. پس درنتیجه می­‌توان راس \(u\) را به مولفه \(H\) اضافه کرد که این با ماکسیمال بودن \(H\) در تناقض است. از تناقض حاصل درستی حکم نتیجه می‌­شود.

نتیجه 3.4.5¶

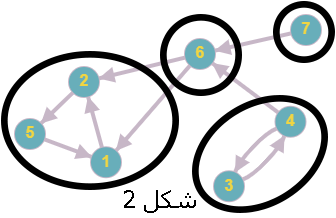
می­‌توان هر گراف جهت‌­دار \(G\) را به مولفه‌­های قویا همبند افراز کرد. شکل 2 گراف جهت­‌داری را نمایش می­‌دهد که مولفه‌­های قویا همبند آن مشخص شده­‌اند.

تعریف 3.4.6 (گراف معکوس)¶

گراف معکوس \(G\) ، گرافی است که از معکوس کردن جهت یال‌های گراف \(G\) بدست می‌آید. توجه کنید یک گراف قویا همبند است اگر و تنها اگر معکوس آن نیز قویا همبند باشد.

تعریف 3.4.7 (گراف فشرده شده مولفه­های قویا همبند)¶

فرض کنید \(G\) ، یک گراف جهت­‌دار دلخواه باشد و گراف جهت­‌دار \(H\) گرافی باشد که هر راس آن متناظر با یک مولفه قویا همبند در \(G\) است و هر مولفه قویا همبند در \(G\) به دقیقا یک راس در \(H\) متناظر شود. اگر \(v\) راسی در \(H\) باشد، مولفه قویا همبند متناظر با راس \(v\) در \(G\) را با \(F(v)\) نمایش می‌­دهیم. اگر \(v\) و \(u\) دو راس از \(H\) باشند، به ازای هر یال جهت‌­دار از رئوس \(F(v)\) به رئوس \(F(u)\) ، یالی جهت­‌دار از \(v\) به \(u\) قرار دارد و همچنین هر یالی که از \(v\) به \(u\) است، متناظر با یالی از رئوس \(F(v)\) به رئوس \(F(u)\) می­‌باشد. در این صورت به \(H\) ، یک گراف فشرده شده مولفه‌­های قویا همبند \(G\) می‌­گوییم.

قضیه 3.4.8¶

صورت قضیه: هر گراف فشرده شده مولفه­‌های قویا همبند، دور ندارد.

اثبات: فرض کنید \(G\) یک گراف جهت‌­دار دلخواه است و \(H\) ، گراف فشرده شده مولفه­‌های قویا همبند \(G\) باشد.از برهان خلف استفاده می‌­کنیم. فرض کنید \(H\) دور داشته باشد و دو راس مانند \(v\) و \(u\) از \(H\) در یک دور قرار داشته باشند. چون از هر راس در یک مولفه قویا همبند به هر راس آن مولفه مسیر هست، پس در نتیجه می‌­توان از هر راس در \(F(v)\) به هر راس در \(F(u)\) رفت و همچنین از هر راس در \(F(u)\) به هر راس در \(F(v)\) مسیری جهت­‌دار وجود دارد (چرا؟) که یعنی رئوس \(F(v)\) و \(F(u)\) باید در یک مولفه قویا همبند قرار بگیرند که این با فرض ماکسیمال بودن مولفه‌­های قویا همبند در تناقض است. پس در نتیجه \(H\) دور ندارد و حکم اثبات می‌­شود.

نتیجه 3.4.9¶

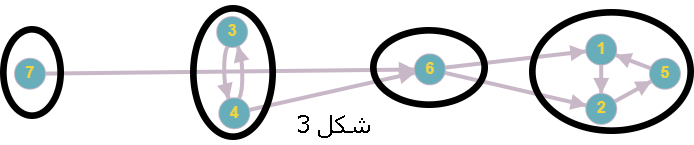
طبق قضیه 3.3.2، می­‌توان رئوس هر گراف فشرده شده مولفه­‌های قویا همبند را توپولوژیک سورت کرد. پس در نتیجه می‌­توان مولفه­‌های قویا همبند هر گراف جهت‌داری را به صورت توپولوژیک سورت کنار هم قرار دهیم، یعنی به این صورت که جهت همه یال­‌هایی که بین دو مولفه متفاوت باشند، به یک سمت باشند (شکل 3).

الگوریتم کساراجو¶

شرح: ابتدا روی کل گراف \(DFS\) می­‌زنیم و هربار هنگام خروج از هر راس آن را در یک پشته می‌­اندازیم (توجه کنید هر چه از راسی دیرتر خارج شویم، در پشته بالاتر قرار می‌گیرد). حال گراف معکوس را درنظر می­‌گیریم و در هر مرحله از بین تمام راس‌های دیده نشده، راسی که در پشته بالاتر از بقیه قرار دارد (مانند \(v\) ) را برداشته و از آن در گراف معکوس، \(DFS\) می‌­زنیم و \(v\) و تمام راس­‌هایی که دیده می‌­شوند (از طریق \(DFS\) زدن از راس \(v\) ) را در یک مولفه جدید قرار می‌­دهیم و این کار را تا پیدا شدن تمام مولفه­‌های قویا همبند ادامه می‌­دهیم. توجه کنید که هنگام \(DFS\) زدن بر روی گراف معکوس، زمانی که راسی دیده می‌­شود، آن را به عنوان دیده شده علامت زده و در سری‌­های بعد از آن \(DFS\) نمی­‌زنیم و یا به آن وارد نمی‌­شویم.

اثبات درستی: برای اثبات این الگوریتم, ابتدا به لم زیر که مشابه آن را در بخش قبل داشتیم توجه کنید.

تعریف می‌کنیم \(f(v)\) به معنای زمان تمام شدن پیمایش برای راس \(v\) . به عبارتی داریم موقعیت یک راس را در پشته مشخص می‌کنیم(هر چه \(f(v)\) بیشتر باشد, راس در پشته در جایگاه پایین‌تری قرار می‌گیرد).

لم ۱: اگر \(f(u) > f(v)\) و به عبارتی راس \(u\) در پشته, بالا تر از راس \(v\) باشد, و همچنین مسیری از \(v\) به \(u\) باشد, آنگاه مسیری از \(u\) به \(v\) نیز وجود دارد.

برهان لم۱: از برهان خلف استفاده می‌کنیم. فرض کنید مسیری از \(v\) به \(u\) است و هیچ مسیری از \(u\) به \(v\) نباشد.

آنگاه چون ما در ابتدا راس \(u\) را در پیمایش دیده‌ایم(چرا؟) و مسیری از \(u\) به \(v\) نیست, پس هیچگاه راس \(v\) را پیمایش نمیکنیم, مگر اینکه پیمایش راس \(u\) تمام شود. از طرفی اگر پیمایش راس \(u\) تمام شود و هنوز راس \(v\) را ندیده باشیم, نتیجه می‌شود که اول \(u\) به پشته اضافه می‌شود و بعد \(v\) به عبارتی \(f(u) < f(v)\) که این خلاف فرض است. پس لم ثابت شد!

حال توجه داشته باشید در هنگام پیمایش گراف معکوس, روی معکوس یال‌ها حرکت می‌کنیم. یعنی عضو بالای پشته که راس \(v\) باشد را برمی‌داریم و روی همه راس‌هایی مثل \(x\) که از \(x\) به \(v\) مسیر هست پیمایش می‌کنیم. در این‌صورت طبق لم۱، راس \(v\) هم به راس \(x\) مسیر دارد!

پس \(v\) و همه رئوسی که در پیمایش گراف معکوس از \(v\) دیده شدند در یک مولفه قرار می‌گیرند!

از طرفی هیچ راس دیگری در این مولفه نیست. زیرا در غیر این صورت اگر راس دیگری در این مولفه قرار می‌گرفت، باید حداقل یک مسیر به \(v\) می‌داشت و جزو ر‌ئوس دیده‌شده از \(v\) شمرده می‌شد.

پیچیدگی الگوریتم¶

در الگوریتم بالا صرفا ۲ بار از \(DFS\) استفاده کردیم, در نتیجه پیچیدگی الگوریتم برابر با \(O(n + m)\) است که \(m, n\) به ترتیب تعداد راس‌ها و یال‌ها می‌باشند.

لم 3.4.10¶

صورت لم: الگوریتم کساراجو، مولفه‌های قویا همبند را به ترتیب توپولوژیک سورت آن‌ها آن‌ها پیدا می‌کند.

اثبات: به استقرا بر روی تعداد مولفه‌های قویا همبند حکم را ثابت می‌کنیم. به ازای یک مولفه که درستی حکم بدیهی است. حال اگر فرض بر درستی حکم به ازای \(n-1\) مولفه باشد، حکم را به ازای \(n\) مولفه ثابت می‌کنیم. اگر به مولفه اولی که در الگوریتم پیدا می‌کنیم (مانند \(H\) ) از مولفه دیگری مانند \(L\) یالی وارد شود، در این صورت در گراف معکوس، از \(H\) به \(L\) یال هست و چون در الگوریتم، \(L\) بعد از \(H\) پیدا می‌شود، پس در هنگام پیمایش \(H\) در گراف معکوس، باید تعدادی از راس‌های \(L\) دیده شوند و در \(H\) قرار گیرند در صورتی که مولفه‌ها نمی‌توانند اشتراک داشته باشند. پس در نتیجه مولفه اولی که پیدا می‌کنیم یالی از سمت مولفه‌های دیگر به آن وارد نمی‌شود و اولین مولفه در توپولوژیک سورت می‌باشد. حال طبق فرض استقرا باقی مولفه‌ها نیز به ترتیب توپولوژیک سورت پیدا می‌شوند (چرا؟) و حکم اثبات می‌شود.

پیاده‌سازی الگوریتم¶

توجه کنید انتها کد، مولفه ها را به ترتیب توپولوژیک سورت آن‌ها خروجی می‌دهیم.

const int MX = 5e5 + 5;

int n, m; /// tedad ras ha va yal ha
vector<int> gr[MX], back_gr[MX], comp[MX]; /// vector mojaverat, vector mojaverat(yal haie barax), moalefe haie ghavian hamband
stack<int> sk; /// moratab kardan ras ha barhasbe tamam shodan dfs
bool mark[MX]; /// array mark baraie check kardane dide shodan ras ha

void dfs(int v){  /// dfs mamoli!
    mark[v] = 1;
    for(int u: gr[v])
                if(!mark[u])
                   dfs(u);
    sk.push(v);
}

void back_dfs(int v, int cnt){  /// dfs roie yal haie barax!
    mark[v] = 1;
    comp[cnt].push_back(v);
    for(int u: back_gr[v])
                if(!mark[u])
                    back_dfs(u, cnt);
}

int main(){
    cin >> n >> m;
    for(int i = 0; i < m; i++){
                int v, u;
                cin >> v >> u; /// shomare ras ha 0-based hast.
                gr[v].push_back(u); /// in vector yal ha ra zakhire mikonad
                back_gr[u].push_back(v); /// in vector barax yal ha ra zakhire mikonad
    }
    for(int i = 0; i < n; i++)
                if(!mark[i])
                    dfs(i);
    fill(mark, mark + n, 0); /// chon mikhahim dfs jadid bezanim, mark ra 0 mikonim.
    int cnt = 0;
    while(sk.size() != 0){ /// stack kheili kond ast. dar inja serfan baraie dark behtar stack estefade shode. behtar ast az vector estefade konid.
                if(!mark[sk.top()]){
                        back_dfs(sk.top(), cnt); /// yek moalefe ra peida mikonim
                        cnt++;
                }
                sk.pop();
    }
    /// moalefe hara be tartib topo sort eshan chap mikonim
    for(int i = 0; i < cnt; i++){
                cout << i << ": ";
                for(auto v: comp[i])
                        cout << v << ' ';
                cout << endl;
    }
    return 0;
}