Segment Tree¶

ساختار¶

هر راس این درخت بیانگر یک بازه از آرایه مورد پرسش است. بچه های هر راس (اگر موجود باشد طبیعتاً دو تا است) بازه پدر خود را نصف می کنند یا به عبارت دیگر اگر بازه راسی $[Begin,End)$ باشد بازه دو پسر چپ و راست آن به ترتیب $[Begin,Middle)$ و $[Middle,End)$ است. راس های بدون بچه هم حاوی تک عضوی از آرایه است.

برای بهتر فهمیدن رابطه ی بین راس ها و بازه ها به شکل زیر نگاه کنید.

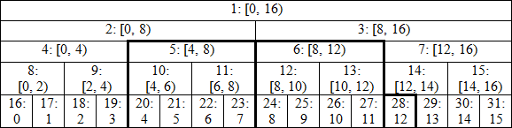
در هر کدام از این راس ها یک اطلاعات مشخصی از بازه متناظر آن راس در آرایه در دسترس است که بسته به استفاده ما از این داده ساختار می تواند متفاوت باشد. برای نمونه اگر دنبال جمع یک بازه از آرایه هستیم هر کدام از راس ها در خود مجموع بازه متناظرشان را ذخیره می کنند.

برای درک بیشتر از این قسمت به شکل زیر نگاه کنید که چطور هر راس مقداری را ذخیره کرده.

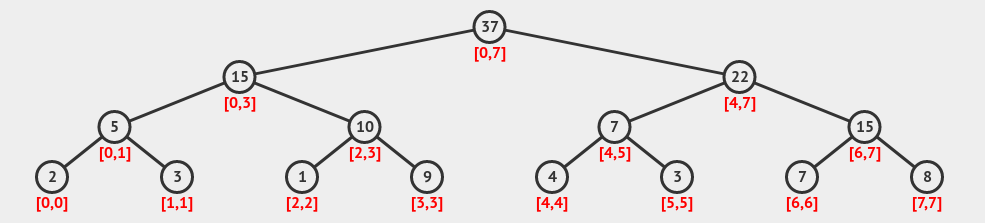
ارتفاع این درخت $lgn$ و تعداد راسی که مورد استفاده قرار می دهد حداکثر $2n$ است بنابراین شما با حافظه $2n$ می توانید این داده ساختار را ذخیره کنید. لازم به ذکر است که بعضی افراد حافظه $4n$ را در نظر می گیرند که بخاطر نوع پیاده سازی برای هر برگ درخت(راس های تک عضوی) دو بچه بدون هیچ مشخصه ای قرار می دهند که باعث می شود حافظه دو برابر شود.

برای شماره گذاری راس ها هم می توان به ریشه عدد یک داد و به بچه های راست و چپ هر راس به ترتیب $2k$ و $2k+1$ داد.

الگوریتم¶

نحوه اجرای این الگوریتم برای انواع سوال های قابل حل با این داده ساختار تقریبا یکسان است و ما با استفاده از یکی از پرسش های مشهور این داده ساختار، به توضیح این الگوریتم می پردازیم.

در ابتدا به ما یک آرایه داده شده و در هر مرحله از ما می خواهند که یا مقدار یک عضو آرایه را تغییر دهیم و یا جمع یک بازه را گزارش دهیم.

void build(int u = 1, int ul = 0, int ur = n){
    if(ur - ul < 2){
        seg[u] = a[ul];
        return;
    }
    int mid = (ul + ur) / 2;
    build(u * 2, ul, mid);
    build(u * 2 + 1, mid, ur);
    seg[u] = seg[u * 2] + seg[u * 2 + 1];
}

void update(int i, int x, int u = 1, int ul = 0, int ur = n){
    seg[u] += x - a[i];
    if(ur - ul < 2){
        a[i] = x;
        return;
    }
    int mid = (ul + ur)/2;
    if(i < mid)
        update(i, x, u * 2, ul, mid);
    else
        update(i, x, u * 2 + 1, mid, ur);
}

int sum(int l, int r, int u = 1, int ul = 0, int ur = n){
    if(x >= ur || ul >= y)return 0;
    if(x <= ul && ur <= y)return seg[u];
    int mid = (ul + ur) / 2;
    return sum(l, r, u * 2, ul, mid) + sum(l, r, u * 2 + 1, mid, ur);
}

انتشار با تاخیر (Lazy propagation)¶

فرض کنید در عملیات اول بجای تغییر یک مقدار، تغییر یک بازه مطرح باشد. به طور مثال به ما بگوید به بازه $L$ تا $R$ دو واحد اضافه کنیم. اگر بخواهیم تمامی عنصر های این بازه را عوض کنیم کار سخت است و تعداد عملیات هایمان بالا می رود. حال با استفاده از تکنیک انتشار با تاخیر می توانیم تعداد عملیات ها را پایین بیاوریم. به این صورت که به ازای هر راس یک مقدار دیگر هم در نظر می گیریم که بر فرض در آرایه Lazy ذخیره می شود. بازه داده شده برای تغییر را مانند روشی که در عملیات دوم برای بازه خواسته شده انجام دادیم افراز می کنیم به بازه های کوچک تر (روی درخت) و مقدار آرایه Lazy تمامی این راس ها (راس هایی که بازه روی آن ها افراز شده) را عوض می کنیم. و هر هنگام که در کل این الگوریتم بر روی راسی از درخت بودیم Lazy آن را به مقدار خود راس اضافه می کنیم و Lazy آن را به Lazy بچه هایش اضافه می کنیم و بعد آن را صفر می کنیم.

void upd(int u, int ul, int ur, int x){
    lazy[u] += x;
    seg[u] += (ur - ul) * x;
}
void shift(int u, int ul, int ur){
    int mid = (ul + ur) / 2;
    upd(u * 2, ul, mid, lazy[u]);
    upd(u * 2 + 1, mid, ur, lazy[u]);
    lazy[u] = 0;
}
void increase(int l, int r, int x, int u = 1, int ul = 0, int ur = n){
    if(l >= ur || ul >= r)return;
    if(l <= ul && ur <= r){
        upd(u, ul, ur, x);
        return;
    }
    shift(u, ul, ur);
    int mid = (ul + ur) / 2;
    increase(l, r, x, u * 2, ul, mid);
    increase(l, r, x, u * 2 + 1, mid, ur);
    seg[u] = seg[u * 2] + seg[u * 2 + 1];
}
int sum(int l, int r, int u = 1, int ul = 0, int ur = n){
    if(l >= ur || ul >= r)return 0;
    if(l <= ul && ur <= r)return seg[u];
    shift(u, ul, ur);
    int mid = (ul + ur) / 2;
    return sum(l, r, u * 2, ul, mid) + sum(l, r, u * 2 + 1, mid, ur);
}